请阅读下列材料：
我们可以通过配方，利用平方的非负性来求出代数式的最值．
例如：①请求出代数式x2+4x-1的最值．
∵x2+4x-1=（x+2）2-5，且（x+2）2≥0，
∴当x=-2时，代数式x2+4x-1有最小值-5．
②请求出代数式-x2-2x+1的最值．
∵-x2-2x+1=-（x+1）2+2，且-（x+1）2≤0．
∴当x=-1时，代数式-x2-2x+1有最大值2．
请根据上述方法，解决下列问题：
（1）当x=-1-1，代数式2x2+4x-3有最 小小（填“大”，“小”）值为 -5-5；
（2）代数式2x2+kx+6有最小值2，求k的值．
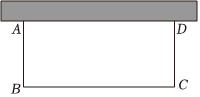
（3）应用拓展：如图，现在有长度24m的围栏，要利用一面墙（墙的最大可用长度为15m）来围成菜园，BC的长度不大于墙的长度，要围成中间有一道围栏的矩形菜园，请问菜园的长BC和宽AB分别为多少时，菜园有最大面积？
【考点】二次函数的应用．
【答案】-1；小；-5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/6 11:0:2组卷：39引用：2难度：0.5
相似题
-
1．某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系．
（1）求出y与x之间的函数关系式；
（2）写出每天的利润W与销售单价x之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？发布：2025/6/16 9:0:1组卷：2829引用：17难度：0.8 -
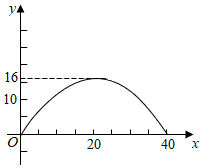2．如图，某抛物线型桥拱的最大高度为16米，跨度为40米，如图所示建立平面直角坐标系，则该抛物线对应的函数关系式为 ．发布：2025/6/16 12:0:1组卷：651引用：3难度：0.8 -
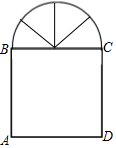3．如图窗户边框的上部分是由4个全等扇形组成的半圆，下部分是矩形，现在制作一个窗户边框的材料总长度为6米．（ π取3）
（1）若设扇形半径为x,请用含x的代数式表示出AB．并求出x的取值范围．
（2）当x为何值时，窗户透光面积最大，最大面积为多少？（窗框厚度不予考虑）发布：2025/6/16 8:0:2组卷：777引用：5难度：0.8
