平面上，Rt△ABC与直径为CE的半圆O如图1摆放，∠B=90°，AC=2CE=m,BC=n,半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转且∠ECD始终等于∠ACB，旋转角记为α（0°≤α≤180°）
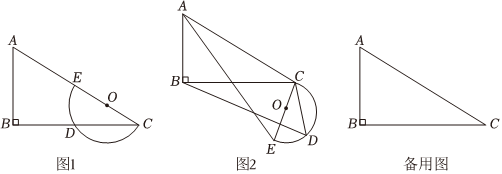
（1）当α=0°时，连接DE，则∠CDE=9090°，CD=n2n2；
（2）试判断：旋转过程中BDAE的大小有无变化，请仅就图2的情形给出证明；
（3）若m=6，n=42，当半圆O旋转至与△ABC的边相切时，直接写出线段BD的长．
n
2
n
2
BD
AE
n
=
4
2
【考点】圆的综合题．
【答案】90；
n
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/7 8:0:9组卷：45引用：3难度：0.3
相似题
-
1．如图1、2，在▱ABCD中，AB=10，AD=15，tan∠BAD=
，点M在AD上由点A向点D运动，过点M在AD的右侧作MP⊥AM，连接PA，PD，使∠MPA=∠BAD，经过点A，M，P作⊙O．43
（1）如图1，若AM=4，则阴影部分的面积为 （结果保留π）；
（2）在点M移动过程中，与ˆAM的比是否为定值？如果是，求出这个比值；如果不是，请说明理由．并求当⊙O与DP相切时AM的长；ˆPM
（3）如图2，当△APD的外心Q在△AMP内部时（包括边界），求在点M移动过程中，点Q经过的路径的长；
（4）当△APD为等腰三角形，并且PD与⊙O相交时，直接写出⊙O截线段PD所得弦的长．（参考数据：sin49°≈，tan37°≈34，cos41°≈34）34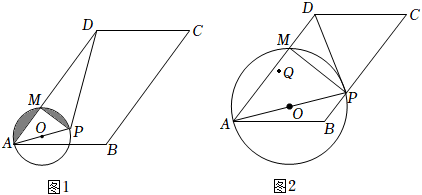
发布：2025/5/25 19:0:2组卷：173引用：1难度：0.1 -
2．如图1，在⊙O中，AB和CD是两条弦，且AB⊥CD，垂足为点E，连接BC，过A作AF⊥BC于F，交CD于点G；
（1）求证：GE=DE；
（2）如图2，连接AC、OC，求证：∠OCF+∠CAB=90°；
（3）如图3，在（2）的条件下，OC交AF于点N，连接EF、EN、DN，若OC∥EF，EN⊥AF，DN=2，求NO的长．17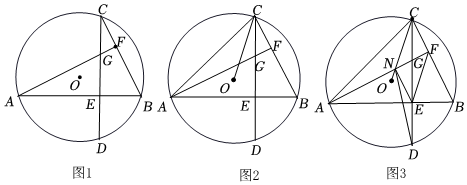
发布：2025/5/25 19:30:2组卷：90引用：1难度：0.1 -
3．如图1，直径AB⊥CD于点E，AB=10，CD=8，点P是CD延长线上异于点D的一个动点，连结AP交⊙O于点Q，连结AC，CQ．
（1）求证：∠P=∠ACQ．
（2）如图2，连结DQ，当DP=2时，求△ACQ和△CDQ的面积之比．
（3）当四边形ACDQ有两边相等时，求DP的长．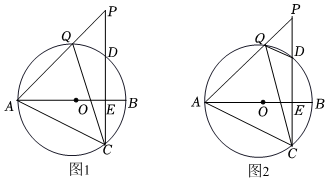
发布：2025/5/25 18:0:1组卷：298引用：2难度：0.5
