如图，在四边形ABCD中，∠ADC=α，∠BCD=β，延长AB到点E，AF是∠DAB的平分线，BG是∠CBE的平分线．
（1）如图1，当AF∥BG时，求证：α+β=180°
（2）如图2，当 α+β＞180°时，直线AF交直线BG于点M，问∠AMB 与α，β之间有何数量关系？写出你的结论并证明；
（3）如果将（2）中的条件 α+β＞180° 改为 α+β＜180°，那么∠AMB与α，β之间又有何数量关系？请直接写出结论，不用证明．
【答案】（1）证明见解答；
（2）2∠AMB=α+β-180°，证明见解答；
（3）2∠AMB=180°-α-β．
（2）2∠AMB=α+β-180°，证明见解答；
（3）2∠AMB=180°-α-β．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 8:0:10组卷：714引用：1难度：0.4
相似题
-
1．已知，四边形ABCD中，∠C+∠D=200°，∠B=3∠A，求∠A和∠B的度数．
发布：2025/6/14 22:0:2组卷：489引用：6难度：0.8 -
2．四边形ABCD中，∠A=145°，∠D=75°．
（1）如图1，若∠B=∠C，试求出∠C的度数；
（2）如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；
（3）如图3，若∠ABC和∠BCD的角平分线交于点E，试求出∠BEC的度数．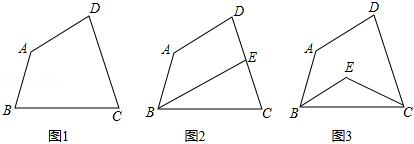
发布：2025/6/14 23:30:1组卷：901引用：7难度：0.3 -
3．正四边形的内角和是 °．
发布：2025/6/14 21:30:2组卷：56引用：3难度：0.8
