（1）问题发现
如图1，在Rt△ABC中，∠A=90°，ABAC=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD．
填空：①PBCD=11；
②∠ACD的度数为45°45°．
（2）拓展探究
如图2，在Rt△ABC中，∠A=90°，ABAC=k.点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B的数量关系以及PB与CD之间的数量关系，并说明理由．
（3）解决问题
如图3，在△ABC中，∠B=45°，AB=42，BC=12，P是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若PA=5，请直接写出CD的长．
AB
AC
PB
CD
AB
AC
2
【考点】三角形综合题．
【答案】1；45°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/26 11:0:1组卷：1545引用：12难度：0.3
相似题
-
1．在等腰Rt△ABC中，∠ACB=90°，AC=BC，D为BC上一点，DE⊥AB于点E，连接AD，F为AD中点，连接CF并延长交AB于点G，连接EF．
（1）如图1，当2GF=FC，GE=时，求Rt△ABC的面积．5
（2）如图2，当BE=AG，判断线段AG2，GE2，CD2之间的数量关系，并说明理由．43
（3）如图3，在等腰Rt△ABC中，∠ACB=90°，AC=BC=2，以AC为边逆时针方向作∠CAR=30°，点M为AR上一点，以CM为边向下构造等腰Rt△CNM，P为CN中点，当AP+CP和最小时，直接写出的值．APCP发布：2025/6/21 21:0:1组卷：428引用：1难度：0.2 -
2．如图，在Rt△ABC中，∠BAC=90°，AB=AC，点D是BC中点，点E是AC边上一动点，连接DE，在DE左侧作Rt△DEF，满足∠DFE=90°，DF=EF，连接AF并延长，交BC于点G．
（1）如图1，若AB=4，AE=1，求DE的长；
（2）如图2，在点E的运动过程中，猜想AF与FG存在的数量关系，并证明你的结论；
（3）如图3，在点E的运动过程中，将AF绕点F逆时针旋转90°，得到A′F，连接A'B，A'D，若AB=4，请直接写出当A'B+A′D取得最小值时，△A′DF的面积．55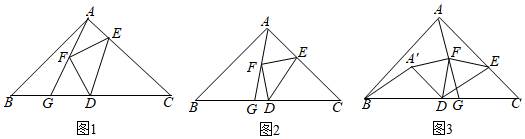
发布：2025/6/21 22:0:1组卷：254引用：2难度：0.5 -
3．已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°．
（1）①求证：AC=BD；
②∠APB=；
（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为，∠APB的大小为．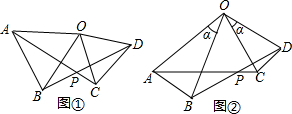
发布：2025/6/22 0:30:2组卷：30引用：1难度：0.5
