在七下的学习中,我们研究了双内角平分线的夹角和内外角平分线的夹角问题.昆昆同学在自主探究的过程中又发现了一类新的问题,他的探究过程如下:
【探索研究】:
(1)如图1,在△ABC中,BM平分∠ABC、CM平分∠ACB,BM,CM相交于点M,若∠A=50°,则∠BMC=115°115°;
【初步应用】:
(2)如图2,在△ABC中,BM平分∠ABC、CM平分∠ACB,BM、CM相交于点M,若将△ABC沿DE折叠使
得点A与点M重合,若∠1+∠2=120°,求∠BMC的度数;
【拓展延伸】:
(3)在四边形ABCD中,AD∥BC,点P在射线CD上运动(点P不与C,D两点重合),连接AP,BP,∠DAP、
∠CBP的角平分线交于点Q,若∠DAP=α,∠CBP=β,直接写出∠Q和a,β之间的数量关系.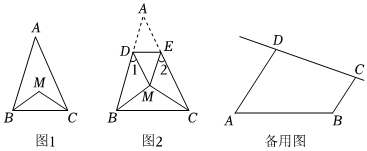
【答案】115°
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/29 8:0:10组卷:201引用:1难度:0.5
相似题
-
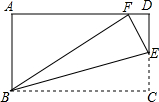 1.如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 .发布:2025/6/18 22:30:2组卷:1821引用:64难度:0.7
1.如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 .发布:2025/6/18 22:30:2组卷:1821引用:64难度:0.7 -
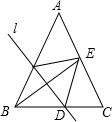 2.如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )发布:2025/6/18 22:30:2组卷:1515引用:43难度:0.5
2.如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )发布:2025/6/18 22:30:2组卷:1515引用:43难度:0.5 -
 3.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为( )发布:2025/6/18 22:30:2组卷:1487引用:48难度:0.7
3.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为( )发布:2025/6/18 22:30:2组卷:1487引用:48难度:0.7


