【问题背景】△ABC中,∠ABC=90°,AB=BC,点D为直线BC上一点.
【初步探究】(1)如图1,当点D在线段BC上时,连接AD,过点A作AE⊥AD于点A,且AD=AE,过点E作EH⊥AC于H点,交AB于F点.求证:EF=AC.

请将证明过程补充完整:
证明:∵AE⊥AD,
∴∠EAD=90°
即∠EAH+∠CAD=90°
∵EH⊥AC,
∴∠AHE=90°,
∴∠EAH+∠AEH=90°( 直角三角形的两锐角互余直角三角形的两锐角互余),
∴∠AEH=∠CAD∠CAD( 同角的余角相等同角的余角相等).
∵△ABC为等腰直角三角形,∠ABC=90°,
∴∠BAC=∠ACB=45°.
在Rt△AHF中,
∠AFE=180°-∠AHF-∠HAF=180°-90°-45°=45°,
∴∠AFE=∠DCA=45°.
在△AEF与△DAC中,
∠AEF=∠DAC ∠AFE=∠DCA (ㅤㅤ)
∴△AEF≌△DAC,
∴EF=AC( 全等三角形的对应边相等全等三角形的对应边相等).
【推广探究】(2)如图2,若点D为边BC延长线上一点,其他条件不变,则(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
【拓展应用】(3)若AC=6,AH=2,其它条件不变时,EH=4或84或8.
∠ AEF =∠ DAC |
∠ AFE =∠ DCA |
( ㅤㅤ ) |
【考点】三角形综合题.
【答案】直角三角形的两锐角互余;∠CAD;同角的余角相等;全等三角形的对应边相等;4或8
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/12 8:0:8组卷:1291引用:1难度:0.5
相似题
-
 1.如图,三角形ABO的三个顶点的坐标分别为O(0,0),A(5,0),B(2,4).
1.如图,三角形ABO的三个顶点的坐标分别为O(0,0),A(5,0),B(2,4).
(1)求三角形OAB的面积;
(2)若O,B两点的位置不变,点M在x轴上,则点M在什么位置时,三角形OBM的面积是三角形OAB的面积的2倍?
(3)若O,A两点的位置不变,点N由点B向上或向下平移得到,则点N在什么位置时,三角形OAN的面积是三角形OAB的面积的2倍?发布:2025/6/17 6:30:2组卷:331引用:2难度:0.3 -
2.(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是;
(2)问题解决:如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.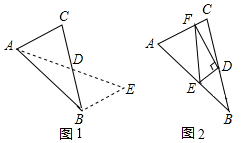 发布:2025/6/17 11:0:1组卷:624引用:7难度:0.4
发布:2025/6/17 11:0:1组卷:624引用:7难度:0.4 -
3.如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
(1)求证:AD=BE;
(2)求∠AEB的度数;
(3)探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM⊥DE于点M,连接BE.
①∠AEB的度数为 °;
②线段DM,AE,BE之间的数量关系为 .(直接写出答案,不需要说明理由)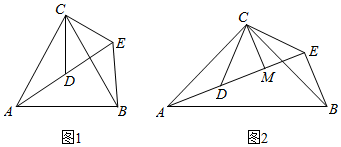 发布:2025/6/17 6:0:2组卷:365引用:3难度:0.6
发布:2025/6/17 6:0:2组卷:365引用:3难度:0.6


