当前位置：
试题详情
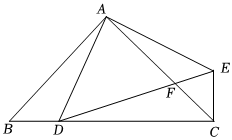如图，在△ABC中，∠BAC=90°，AB=AC=4，D是BC边上一点，连接AD，以AD为直角边向右作等腰直角三角形ADE，其中∠DAE=90°．
（1）连接CE，求证：△ABD≌△ACE；
（2）当BD为何值时，△ADE的周长最小．
【答案】（1）证明见解析部分；
（2）当BD=时，△ADE的周长最短．
（2）当BD=
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/21 8:0:10组卷：200引用：2难度：0.5
相似题
-
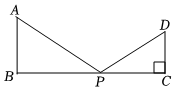1．如图，AB⊥BC，CD⊥BC，垂足分别为B，C，P为线段BC上一点，连结PA，PD．已知AB=5，DC=4，BC=12，则AP+DP的最小值为 ．发布：2025/6/10 3:0:1组卷：411引用：4难度：0.6 -
2．如图，在矩形ABCD中，AB=10，BC=5．若点M、N分别是线段AC，AB上的两个动点，则BM+MN的最小值为（ ）发布：2025/6/10 5:30:2组卷：4544引用：55难度：0.9 -
3．如图，Rt△ABC中，∠BAC=90°，AB=AC=4，点E为AB边上一点，AE=3，点D为BC边的中点，连接AD，点F为线段AD上的动点，连接FE，FB，则FE+FB的最小值为 ．发布：2025/6/10 3:0:1组卷：920引用：5难度：0.6
