问题背景：“对角互补”是经典的四边形模型，解决相应问题，通常会涉及到旋转构造、全等三角形的证明等综合性较高的几何知识．如果问题中有“45°，60°”角度出现，一般会和等腰直角三角形、正方形、等边三角形等特殊图形结合起来考查．
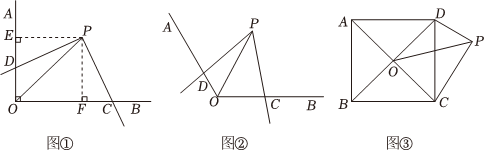
（1）【问题解决】如图①，∠AOB=∠CPD=90°，OP平分∠AOB，小明同学从P点分别向OA，OB作垂线PE，PF，由此得到正方形OFPE，与△PED全等的三角形是 △PFC△PFC；
（2）【问题探究】如图②，若∠AOB=120°，∠CPD=60°，OP平分∠AOB，OD=1，OC=2，求OP的长；
（3）【拓展延伸】如图③，点P是正方形ABCD外一点，∠CPD=90°，∠PCD=30°，对角线AC，BD交于点O，连接OP，且OP=6+2，求正方形ABCD的面积．
6
+
2
【考点】四边形综合题．
【答案】△PFC
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/25 19:0:2组卷：472引用：1难度：0.2
相似题
-
1．如图1，正方形ABCD中，AC为对角线，点P在线段AC上运动，以DP为边向右作正方形DPFE，连接CE；
【初步探究】
（1）则AP与CE的数量关系是 ，AP与CE的夹角度数为 ；
【探索发现】
（2）点P在线段AC及其延长线上运动时，如图1，图2，探究线段DC，PC和CE三者之间的数量关系，并说明理由；
【拓展延伸】
（3）点P在对角线AC的延长线上时，如图3，连接AE，若AB=，AE=22，求四边形DCPE的面积．213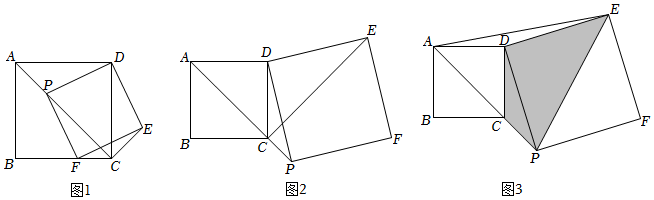
发布：2025/5/26 8:0:5组卷：2163引用：9难度：0.3 -
2．阅读与思考
平移是初中几何变换之一，它可以将线段和角平移到一个新的位置，从而把分散的条件集中到一起，使问题得以解决．平移包括以下三个方面的应用：一、分散的条件集中；二、复杂图形变得简单明了；三、转化题目的形式．以下面例题来说明．
如图1，在正方形中ABCD中，E，F，G分别是BC，CD，AD上的点，GE⊥BF于点O，那么GE=BF．
证明过程如下：
∵GE⊥BF于点O，
∴∠GOB=90°，
过点A作AH∥GE交BC于点H，交BF于点M．
∴∠AMB=∠GOB=90°，
∴∠ABM+∠BAM=90°，
∵四边形ABCD为正方形，
∴AG∥HE，AB=BC，∠ABC=∠C=90°，
∴∠ABM+∠FBC=∠ABC=90°，
∴∠BAM=∠FBC，
∴△ABH≌△BCF（依据1），
∴AH=BF，
∵AH∥GE，AG∥HE，
∴四边形AHEG为平行四边形（依据2），
∴AH=GE，
∴GE=BF．
【阅读理解】填空：上述阅读材料中“依据1”是 ，“依据2”是 ．
【迁移尝试】如图2，在5×6的正方形网格中，点A，B，C，D为格点，AB交CD于点M．则∠AMC的度数为 ；
【拓展应用】如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N．求∠DMC的度数．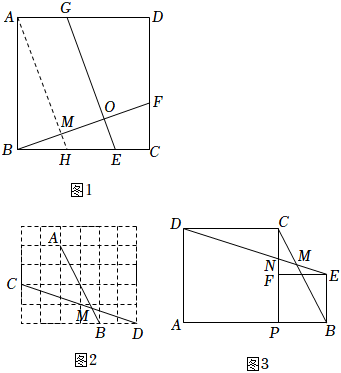
发布：2025/5/26 9:0:1组卷：217引用：2难度：0.3 -
3．在正方形ABCD中，对角线AC、BD相交于点O，F是正方形ABCD内一点，∠BFC=90°，将△BFC绕点C按顺时针方向旋转一定角度得到△DEC，点B、F的对应点分别为点D、E，则直线EF经过点O．
【方法感知】如图①，当点F在△AOB内时，过点D作DG⊥DE交EF于点G，则∠DGE的大小为 度，DE、OE、OF的数量关系为 ．
【类比迁移】如图②，当点F在△COD内时，试判断DE、OE、OF之间的数量关系，并说明理由．
【拓展应用】如图③，将正方形ABCD改为菱形，对角线AC、BD相交于点O，F是△COD内一点，∠BFC=90°．若将△BFC绕点C按顺时针方向旋转60°得到△DEC，点B、F的对应点分别为点D、E．若DE=2，则OE+OF=．2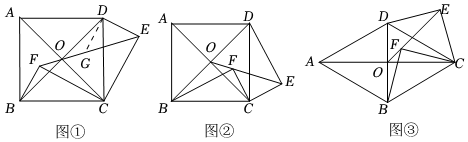
发布：2025/5/26 7:30:2组卷：160引用：1难度：0.3
