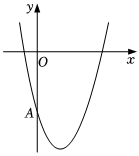
如图，在平面直角坐标系中，点A（0，-3）在抛物线y=x2+bx+c上，其对称轴是直线x=2．点P、Q为该抛物线上的点，其横坐标分别为m,m+3，设该抛物线在点P与点Q之间部分（含点P和点Q）的图象记为G，图象G的最高点与最低点的纵坐标之差为h.
（1）求该抛物线的解析式；
（2）点P的纵坐标为2时，求点Q的坐标；
（3）当图象G的最低点是该抛物线的顶点时，①求h与m之间的函数关系式；②当h=5时，直接写出m的值．
【答案】（1）抛物线的解析式为y=x2-4x-3；
（2）点Q的坐标为（2，-7）或（8，29）；
（3）①h与m之间的函数关系式为h=
；
②m=2-或m=-1+．
（2）点Q的坐标为（2，-7）或（8，29）；
（3）①h与m之间的函数关系式为h=
m 2 - 4 m + 4 （ - 1 ≤ m ≤ 1 2 ） |
m 2 + 2 m + 1 （ 1 2 ≤ m ≤ 2 ） |
②m=2-
5
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/22 8:0:9组卷：218引用：4难度：0.4
