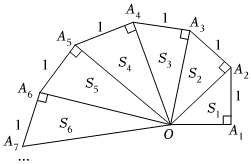
细心观察图形，认真分析各式，然后解答下列问题：
OA22=（1）2+1=2，S1=12，（S1是Rt△A1A2O的面积）；
OA23=（2）2+1=3，S2=22，（S2是Rt△A2A3O的面积）；
OA24=（3）2+1=4，S3=32，（S3是Rt△A3A4O的面积）；
…
（1）填空：OA210=1010，S10=102102；
（2）请用含有n（n为正整数）的式子填空：OA2n=nn，Sn=n2n2；
（3）我们已经知道（13+3）（13-3）=4，因此将813-3分子、分母同时乘以（13+3），分母就变成了4，请仿照这种方法求1S1+S2+1S2+S3+1S3+S4+…+1S99+S100的值；
O
A
2
2
=
（
1
）
2
+
1
=
2
S
1
=
1
2
O
A
2
3
=
（
2
）
2
+
1
=
3
S
2
=
2
2
O
A
2
4
=
（
3
）
2
+
1
=
4
S
3
=
3
2
O
A
2
10
10
2
10
2
O
A
2
n
n
2
n
2
（
13
+
3
）
（
13
-
3
）
=
4
8
13
-
3
（
13
+
3
）
1
S
1
+
S
2
+
1
S
2
+
S
3
+
1
S
3
+
S
4
+
…
+
1
S
99
+
S
100
【答案】10；；n；
10
2
n
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/8 8:0:1组卷：479引用：4难度：0.5
