如图，在△ABC中，∠ABC=30°，AB=AC，点O为BC的中点，点D是线段OC上的动点（点D不与点O，C重合），将△ACD沿AD折叠得到△AED，连接BE．
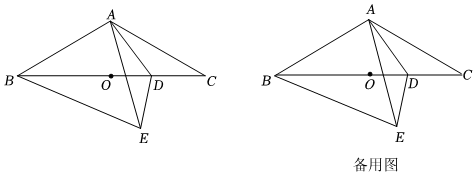
（1）当AE⊥BC时，∠AEB=6060°；
（2）探究∠AEB与∠CAD之间的数量关系，并给出证明．
【考点】翻折变换（折叠问题）；等腰三角形的性质．
【答案】60
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/19 8:0:9组卷：74引用：2难度：0.5
相似题
-
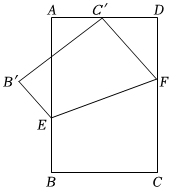1．如图所示，长宽比为3：2的矩形ABCD，将矩形ABCD沿着EF折叠，使点C落到宽AD的中点C′，点B落到点B′处，则tan∠EFC=．发布：2025/5/22 9:0:1组卷：481引用：2难度：0.5 -
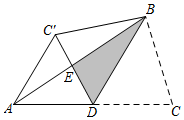2．如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD翻折，得到△BDC′，DC'与AB交于点E，连接AC′，若AD=AC′=2，BD=3，则点D到BC的距离为（ ）发布：2025/5/22 11:0:1组卷：1711引用：8难度：0.1 -
3．如图，在矩形ABCD中，已知AB=10，AD=6，动点P从点D出发，以每秒2个单位的速度沿线段DC向终点C运动，运动时间为t秒，连接AP，把△ADP沿着AP翻折得到△AEP．作射线PE与边AB交于点Q，当QE=QB时，t= s.发布：2025/5/22 9:30:1组卷：794引用：6难度：0.1
