综合与实践
数学活动课上,同学们以对角互补的四边形为活动主题,开展了如下探究.
问题探究
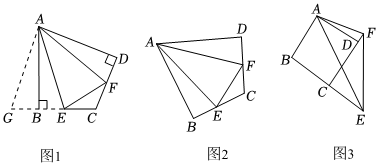
(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=12∠BAD.请探究线段EF,BE,FD之间的数量关系.下面是学习委员琳琳的解题过程,请将余下内容补充完整.
解:延长EB到点G,使得BG=DF,连接AG.
在△ABG和△ADF中,AB=AD ∠ABG=∠ADF=90° BG=DF
∴△ABG≌△ADF(SAS),∴AG=AF,∠BAG=∠DAF,
∴∠BAG+∠BAE=∠DAF+∠BAE.
∵∠EAF=12∠BAD.∴∠GAE=∠EAF.
……
问题迁移
(2)班长李浩同学发现在如图2所示的四边形ABCD中,若AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,∠EAF=12∠BAD,且(1)中的结论仍然是成立的,请你写出结论并完成证明过程;
拓展应用
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=12∠BAD.请探究线段EF,BE,FD之间的数量关系,并说明理由.
1
2
AB = AD |
∠ ABG =∠ ADF = 90 ° |
BG = DF |
1
2
1
2
1
2
【考点】四边形综合题.
【答案】(1)见解析;
(2)EF=BE+FD,证明见解析;
(3)EF=BE-FD,理由见解析.
(2)EF=BE+FD,证明见解析;
(3)EF=BE-FD,理由见解析.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/18 7:0:2组卷:11引用:3难度:0.3
相似题
-
1.在▱ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,分别过点E,F作EG∥DF,GF∥AD.
(1)如图1.求证:四边形EDFG是菱形.
(2)如图2,连接AG,DG,DG与EF相交于点O,若∠AGD=90°,求证:AD=2AB.
(3)如图3.连接DG交EF于点O,连接OC,若∠ABC=90°.AB=6,BC=10,求OC的长.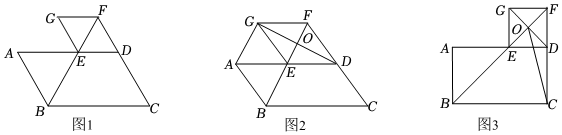 发布:2025/6/14 13:30:1组卷:34引用:1难度:0.1
发布:2025/6/14 13:30:1组卷:34引用:1难度:0.1 -
2.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
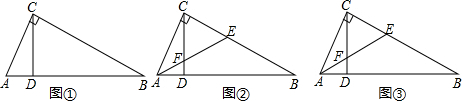
(1)求证:CD⊥AB.
(2)如图②,若∠BAC的平分线分别交BC,CD于点E,F,求证:∠AEC=∠CFE;
(3)如图③,若E为BC上一点,AE交CD于点F,BC=3CE,AB=4AD,S△ABC=36.
①求S△CEF-S△ADF的值;
②四边形BDFE的面积是 .发布:2025/6/14 13:30:1组卷:80引用:2难度:0.1 -
 3.如图,在平面直角坐标系内,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E在BC边上,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
3.如图,在平面直角坐标系内,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E在BC边上,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点C、E、F的坐标;
(2)求EF的长度;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.发布:2025/6/14 13:0:6组卷:116引用:1难度:0.2


