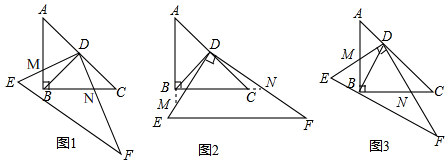
（1）如图1，将含30°的三角板DFF的直角顶点D放置在含45°的直角三角板ABC的斜边AC的中点位置上，两直角边分别交AB、BC于M、N，利用三角形的全等，发现DM与DN数量关系是 DM=DNDM=DN；若AB=5，BM=x,BN=y,y与x的函数关系式为：y=5-xy=5-x；
（2）若将三角板DEF绕顶点D旋转，两直角边分别与AB、BC的延长线交于M、N，如图2，（1）中的DM与DN数量关系是否改变？并说明理由；
（3）若将三角板DEF的顶点D从中点处沿CA方向平移、旋转至△ADB≌△CND，如图3，其余条件不变，求证：BM=BN．
【答案】DM=DN；y=5-x
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/13 3:0:11组卷：205引用：4难度：0.7
相似题
-
1．阅读理解
图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C'DE叠放在一起（C与C'重合）的图形．
操作与证明：
（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD、BE，如图2，在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
（2）若将图1中的△C′DE绕点C按顺时针方向任意旋转一个角度α，连接AD、BE，如图3，图3中线段BE与AD之间具有怎样的大小关系？证明你的结论；
猜想与发现：
（3）根据上面的操作和思考过程，请你猜想当α为 度时，线段AD的长度最大，当α为某个角度时，线段AD的长度最小，最小是 ．发布：2025/6/8 2:30:2组卷：36引用：2难度：0.3 -
2．把△ABC绕着点A顺时针旋转α，得到△ADE．
（1）如图1，当点D恰好在CB的延长线上时，若α=40°，求∠ADE的度数．
（2）如图2，当点E恰好在CB的延长线上时，求证：EA平分∠DEC．
（3）如图3，连接EB，如果BC=BE，连接CE与AD的延长线交于点F，直接写出∠F的度数（用含α的式子表示）．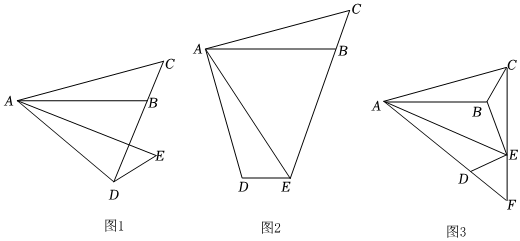
发布：2025/6/8 2:0:5组卷：6引用：1难度：0.1 -
3．如图，两个形状，大小完全相同的含有30°、60°的三角板如图放置，PA、PB与直线MN重合，且三角板PAC，三角板PBD均可以绕点P逆时针旋转．
（1）①如图1，∠DPC=度．
②我们规定，如果两个三角形只要有一组边平行，我们就称这两个三角形为“孪生三角形”，如图1，三角板BPD不动，三角板PAC从图示位置开始每秒10°逆时针旋转一周（0°＜旋转＜360°），问旋转时间t为多少时，这两个三角形是“孪生三角形”．
（2）如图3，若三角板PAC的边PA从PN外开始绕点P逆时针旋转，转速3°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速2°/秒，在两个三角板旋转过程中，（PC转到与PM重合时，两三角板都停止转动）．设两个三角板旋转时间为t秒，以下两个结论：①为定值；②∠BPN+∠CPD为定值，请选择你认为对的结论加以证明．∠CPD∠BPN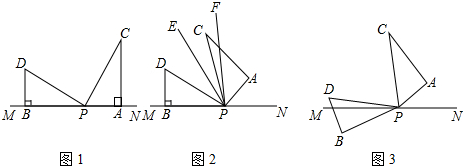
发布：2025/6/8 0:0:1组卷：1321引用：4难度：0.2
