课题学习：平行线的“等角转化”功能．

如图，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数． ∵∠B= ∠EAB ∠EAB ，∠C= ∠DAC ∠DAC ． 又∵∠EAB+∠BAC+∠DAC=180°， ∴∠B+∠BAC+∠C=180°．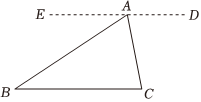

（1）阅读并补充推理过程．
解题反思：
从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决．
方法运用：
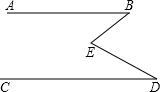
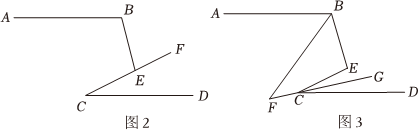
（2）如图2，已知AB∥CD，∠BEC=100°，求∠B-∠C 的度数．（提示：过点E作AB或CD的平行线．）
深化拓展：
（3）如图3，AB∥CD，BF、CG分别平分∠ABE，∠DCE，且所在直线交于点F，∠E=100°，求∠F的度数．