(1)【学习心得】
小宸同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
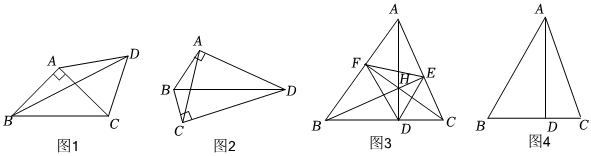
例如:如图1,在△ABC中,∠BAC=90°,AB=AC=AD,求∠BDC 的度数,若以点A为圆心,AB为半径作辅助圆⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC=4545°.
(2)【问题解决】
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BAC=26°,求∠BDC 的度数.小宸同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:△ABD 的外接圆就是以BD的中点为圆心,12BD长为半径的圆;△BCD的外接圆也是以BD的中点为圆心,12BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BDC 的度数,请运用小底的思路解决这个问题.
(3)【问题拓展】
①如图3,△ABC的三条高AD、BE、CF相交于点H,求证:∠EFC=∠DFC.
②如图4,在△ABC中,∠BAC=45°,AD是BC边上的高,且BD=3,CD=1,直接写出AD的长.
1
2
1
2
【考点】圆的综合题.
【答案】45
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/9 9:0:1组卷:1211引用:7难度:0.1
相似题
-
1.如图1,以点O为圆心,半径为4的圆交x轴于A,B两点,交y轴于C,D两点,点P为劣弧AC上的一动点,延长CP交x轴于点E;连接PB,交OC于点F.
(1)若点F为OC的中点,求PB的长;
(2)求CP•CE的值;
(3)如图2,过点O作OH∥AP交PD于点H,当点P在弧AC上运动时,连接AC,PC.试问△APC与△OHD相似吗?说明理由;的值是否保持不变?若不变,试证明,求出它的值;若发生变化,请说明理由.APDH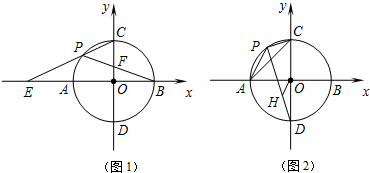 发布:2025/6/24 18:30:1组卷:272引用:1难度:0.5
发布:2025/6/24 18:30:1组卷:272引用:1难度:0.5 -
2.下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.画法:
(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.则直线AD就是过点A的圆的切线.
请回答:①这种画法是否正确 (是或否);
②你判断的依据是:.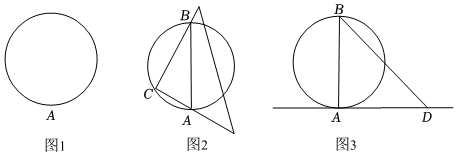 发布:2025/6/25 8:0:1组卷:19引用:1难度:0.4
发布:2025/6/25 8:0:1组卷:19引用:1难度:0.4 -
 3.如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为.5
3.如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为.5
(1)比较线段AB与CD的大小;
(2)求A、B、C、D四点的坐标;
(3)过点D作⊙O′的切线,试求这条切线的解析式.发布:2025/6/24 20:0:2组卷:43引用:1难度:0.5


