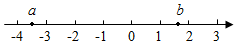阅读材料
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．也就是说，|4-（-3）|表示4与-3之差的绝对值，实际上也可理解为4与-3两数在数轴上所对的两点之间的距离．
比如|x+3|可以写成|x-（-3）|，它的几何意义是数轴上表示数x的点与表示数-3的点之间的距离
再举个例子：等式|x-1|=1的几何意义可表示为：在数轴上表示数x的点与表示数1的点的距离等于1，这样的数x可以是0或2．
解决问题
（1）|4-（-3）|=

7

7

．
（2）若|x+3|=7，则x=

4或-10

4或-10

；若|x+3|=|x-1|，则x=

-1

-1

．
（3）|x+3|+|x-1|表示数轴上有理数x所对的点到-3和1所对的两点距离之和．请你利用数轴，找出所有符合条件的整数x,使得|x+3|+|x-1|=4．
（4）若x表示一个有理数，则|x+5|+|x+3|+|x-1|有最小值吗？若有，请直接写出最小值．若没有，说出理由．