 阅读理解:
阅读理解:
若x满足(30-x)(x-10)=160,求(30-x)2+(x-10)2的值.
解:设30-x=a,x-10=b,则(30-x)(x-10)=ab=160,
a+b=(30-x)+(x-10)=20,
(30-x)2+(x-10)2=a2+b2=(a+b)2-2ab=202-2×160=80.
解决问题:
(1)若x满足(50-x)(x-40)=2,则(50-x)2+(x-40)2=9696.
(2)若x满足(x-2024)2+(x-2022)2=2000,求(x-2024)•(x-2022)的值;
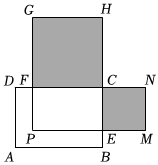
(3)如图,在长方形ABCD中,AB=10,BC=6,E,F分别是BC,CD上的点,且BE=DF=x,分别以FC,CE为边在长方形ABCD外侧作正方形CFGH和正方形CEMN,若长方形CEPF的面积为45,求图中阴影部分的面积.
【考点】整式的混合运算—化简求值;完全平方公式的几何背景.
【答案】96
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/1 5:0:1组卷:180引用:2难度:0.5


