在正方形ABCD中，O是AD的中点，点P从A点出发沿A→B→C→D的路线匀速运动，移动到点D时停止．
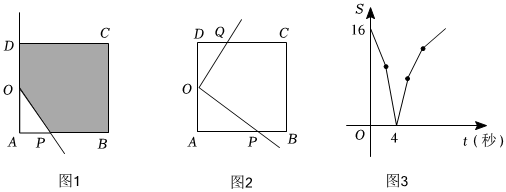
（1）如图1，若正方形的边长为12，点P的运动速度为2单位长度/秒，设t秒时，正方形ABCD与∠POD重叠部分的面积为y.
①求当t=4时，y的值．
②求y关于t的函数解析式．
（2）如图2，若点Q从D出发沿D→C→B→A的路线匀速运动，移动到点A时停止．P、Q两点同时出发，点P的速度大于点Q的速度．设t秒时，正方形ABCD与∠POQ（包括边缘及内部）重叠部分的面积为S，S与t的函数图象如图3所示．
①P，Q两点在第 44秒相遇；正方形ABCD的边长是 44；
②当t为何值时，重叠部分面积S等于9？
【考点】四边形综合题．
【答案】4；4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 12:0:1组卷：75引用：2难度：0.5
相似题
-
1．如图所示，在平行四边形ABCD中，∠DAC=60°，点E是BC边上一点，连接AE，AE=AB，点F是对角线AC边上一动点，连接EF．
（1）如图1，若点F与对角线交点O重合，已知BE=4，OC：EC=5：3，求AC的长度；
（2）如图2，若EC=FC，点G是AC边上一点，连接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求证：BG+EG=DC．
（3）如图3，若BE=4，CE=，将EF绕点E逆时针旋转90°得EF'，请直接写出当AF'+433BF'取得最小值时△ABF′的面积．12
发布：2025/6/21 23:30:2组卷：402引用：1难度：0.4 -
2．平行四边形ABCD中，AB⊥AC，点E在边AD上，连BE．
（1）如图1，AC交BE于点G，若BE平分∠ABC，且∠DAC=30°，CG=2，请求出四边形EGCD的面积；
（2）如图2，点F在对角线AC上，且AF=AB，连BF，过点F作FH⊥BE于H，连AH并延长交CD于点M，点N在边AD上，连MN．若AN=BF，2∠NMD=∠DAC+∠HBF，求证：HF+AH=AC．2
（3）如图3，线段PO在线段BE上运动，点R在边BC上，连接CQ、PR．若BE平分∠ABC，∠DAC=30°，AB=，PQ=3，BC=4BR．请直接写出线段CQ+PQ+PR的和的最小值以及此时△CQE的面积．32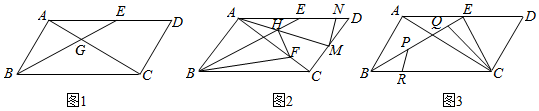
发布：2025/6/22 1:0:1组卷：261引用：3难度：0.5 -
3．如图，四边形ABCD是平行四边形，点E、F在BC上，且CF=BE，连接DE，过点F作FG⊥AB于点G．
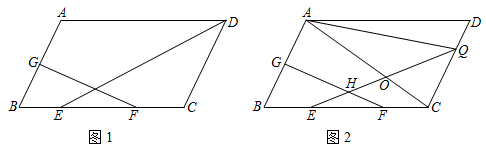
（1）如图1，若∠B=60°，DE平分∠ADC，且CD=2CF，CD=6，求平行四边形ABCD的面积．3
（2）点H在GF上，且HE=HF，延长EH交AC，CD于点O，Q，连接AQ，若AC=BC=EQ，∠EQC=45°，求证：CE=BG+DQ．2发布：2025/6/21 23:0:2组卷：155引用：1难度：0.1
