如图1,嘉琪想知道一堵墙上点A距地面的高度AO(墙与地面垂直,即AO⊥OD),但又不便直接测量,于是嘉琪同学设计了下面的方案:
第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹角∠ABO;
第二步:使直杆顶端竖直缓慢下滑,直到∠DCODCO=∠ABO.标记此时直杆的底端点D;
第三步:测量 ODOD的长度,即为点A的高度.
(1)请你先补全方案,再利用所学的全等三角形的知识说明这样设计的理由.
(2)如图2,设AB与CD交于点E,善于观察和思考的明明同学猜想线段AE=DE,你同意明明的观点吗?说明理由.

【考点】全等三角形的应用.
【答案】DCO;OD
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/31 15:0:9组卷:115引用:4难度:0.7
相似题
-
 1.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )发布:2025/5/23 16:0:1组卷:393引用:3难度:0.5
1.如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )发布:2025/5/23 16:0:1组卷:393引用:3难度:0.5 -
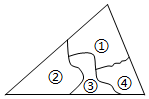 2.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )发布:2024/12/15 21:30:2组卷:4329引用:31难度:0.5
2.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )发布:2024/12/15 21:30:2组卷:4329引用:31难度:0.5 -
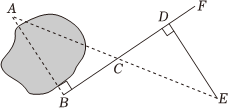 3.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )发布:2024/12/18 6:0:2组卷:4234引用:38难度:0.5
3.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )发布:2024/12/18 6:0:2组卷:4234引用:38难度:0.5


