问题提出
如图1，在△ABC中，AB=BC，点D是边BC上一点，△ADE是等腰三角形，AD=DE，∠ADE=∠B=α（0＜α≤90°），DE交AC于点F，探究∠DCE与α的数量关系．
问题探究
（1）先将问题特殊化，如图2，当α=90°时，直接写出∠DCE的大小；
（2）再探究一般情形，如图1，求∠DCE与α的数量关系．
问题拓展
将图1特殊化，如图3，当α=60°时，若CDBD=12，求CFAF的值．
CD
BD
=
1
2
CF
AF
【考点】相似形综合题．
【答案】（1）135°；
（2）∠DCE=90°+α；
问题拓展：．
（2）∠DCE=90°+
1
2
问题拓展：
2
7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/17 7:0:9组卷：290引用：2难度：0.1
相似题
-
1．（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，点G，F分别在边CD，AB上，GF⊥AE．
①求证：DQ=AE；
②推断：的值为；GFAE
（2）类比探究：如图（2），在矩形ABCD中，=k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的数量关系，并说明理由；BCAB
（3）拓展应用：在（2）的条件下，连接CP，当k=时，若tan∠CGP=23，GF=234，求CP的长．10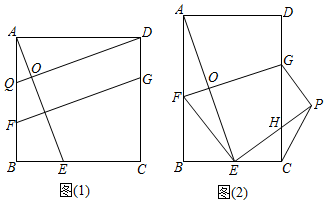
发布：2025/6/22 14:30:2组卷：5190引用：13难度：0.1 -
2．已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持∠ABP=90°不变，BP边与直线l相交于点P．
（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；
（2）请利用如图1所示的情形，求证：=ABPB；OMBM
（3）若AO=2，且当MO=2PO时，请直接写出AB和PB的长．6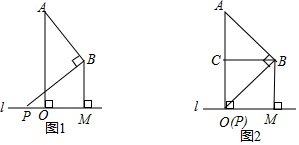
发布：2025/6/22 15:30:1组卷：1012引用：2难度：0.1 -
3．有一副直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=
．将这副直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．43
（1）如图2，当三角板DEF运动到点D与点A重合时，设EF与BC交于点M，则∠EMC=度；
（2）如图3，在三角板DEF运动过程中，当EF经过点C时，求FC的长；
（3）在三角板DEF运动过程中，设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式，并求出对应的x取值范围．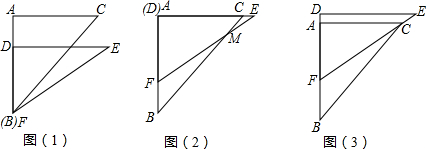
发布：2025/6/22 11:0:2组卷：1820引用：17难度：0.5
