问题情境：

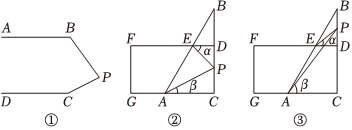
（1）如图①，已知AB∥CD，∠PBA=125°，∠PCD=155°，求∠BPC的度数．
佩佩同学的思路：过点P作PN∥AB，进而PN∥CD，由平行线的性质来求∠BPC，求得∠BPC=

80°

80°

；
问题迁移：
（2）图②，图③均是由一块三角尺和一把直尺拼成的图形，三角尺的两直角边与直尺的两边重合，∠ACB=90°，DF∥CG，AB与FD相交于点E，有一动点P在边BC上运动，连接PE，PA，记∠PED=∠α，∠PAC=∠β．
①如图②，当点P在C，D两点之间运动时，请直接写出∠APE与∠α，∠β之间的数量关系；
②如图③，当点P在B，D两点之间运动时，∠APE与∠α，∠β之间有何数量关系？请说明理由．
拓展延伸：
（3）当点P在C，D两点之间运动时，若∠PED，∠PAC的平分线EN，AN相交于点N，请直接写出∠ANE与∠α，∠β之间的数量关系．