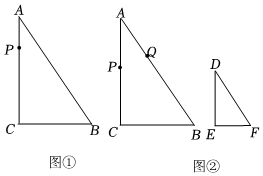
如图，在Rt△ABC中，∠C=90°，BC=6cm,AC=8cm,AB=10cm.现有一动点P，从点A出发，沿着三角形的边AC→CB→BA运动，回到点A停止，速度为2cm/s.设运动时间为t s.
（1）当0≤t≤4时，AP=2t cm2t cm；当7≤t≤12时，AP=（24-2t）cm（24-2t）cm；
（2）如图①，当t=112s或192s112s或192s时，△APC的面积等于△ABC面积的一半；
（3）如图②，在△DEF中，∠E=90°，DE=4cm,DF=5cm,∠D=∠A．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好△APQ与△DEF全等，请直接写出点Q的运动速度．
11
2
19
2
11
2
19
2
【考点】三角形综合题．
【答案】2t cm；（24-2t）cm；s或s
11
2
19
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/19 8:0:9组卷：351引用：1难度：0.3
相似题
-
1．在Rt△ABC中，∠BAC=90°，AB=AC．
（1）如图1，若BM⊥AN于点M，CN⊥AN于点N，求证：CN=AM．
（2）如图2，点A，B分别在y轴和x轴上，直角边AC交x轴于点D，斜边BC交y轴于点E，若C点的横坐标为-2，直接写出点A的坐标．
（3）如图3，若B（-5，0），以OA为直角边在第一象限作Rt△AOD，且AD=AO，连接CD交y轴于P，问当点A在y轴的正半轴上运动时，AP的长度是否变化？若变化，请说明理由，若不变化，求出AP的长度．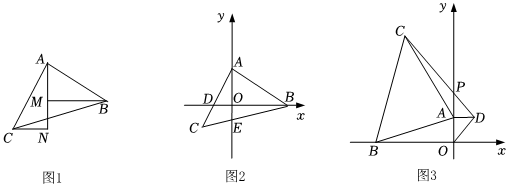
发布：2025/6/13 3:30:1组卷：40引用：1难度：0.3 -
2．如图1，已知，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D在AB上且
，点P，Q分别从点D，B出发沿线段DB，BC向终点B，C匀速移动，P，Q两点同时出发，同时到达终点．设BQ=x,AP=y.BD=154
（1）求AD的值．
（2）求y关于x的函数表达式．
（3）如图2，过点P作PE⊥AC于点E，连结PQ，EQ．
①当△PEQ为等腰三角形时，求x的值．
②过D作DF⊥BC于点F，作点F关于EQ的对称点F'，当点F'落在△PQB的内部（不包括边界）时，则x的取值范围为 ．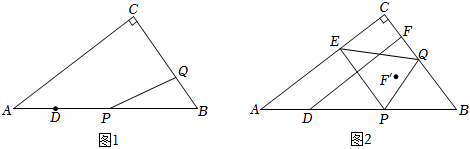
发布：2025/6/13 1:30:1组卷：84引用：3难度：0.1 -
3．在等腰△ABC中，AB=AC，∠BAC=120°，D、E、F分别为线段BC、AB、AC上的点，∠AEF=∠CAD，AD交EF于点G．
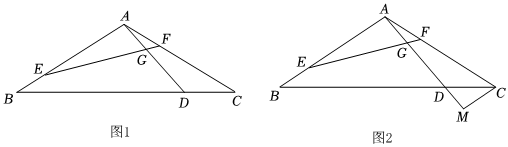
（1）如图1，求∠AGE的度数；
（2）如图2，已知BE=AF，点M在AD的延长线上，AM=EF，连接CM．
①求证：CM∥AB；②若，直接写出ADEF=45的值为 ．CMAB发布：2025/6/13 1:30:1组卷：64引用：2难度：0.1
