已知，点A的坐标是（8，0），点B的坐标是（0，6），点C与点A关于y轴的对称点，动点P，Q分别在线段BC，AC上（点P与点B，C不重合），且满足∠BQP=∠BCA．
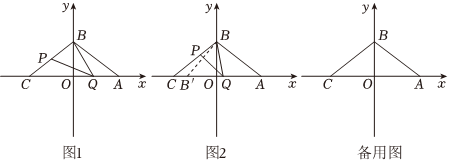
（1）点C的坐标为 （-8，0）（-8，0）上，线段AB的长度=1010．
（2）如图1，当△BPQ为等腰三角形时，求点Q的坐标．
（3）如图2，做点B关于PQ的对称点B'，当点B'落在△ABC的边上时，点B'的坐标为 （-5.76，1.68）或（-4.5，1.75）（-5.76，1.68）或（-4.5，1.75）．（直接写出答案）
【考点】几何变换综合题．
【答案】（-8，0）；10；（-5.76，1.68）或（-4.5，1.75）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/27 4:0:8组卷：14引用：2难度：0.2
相似题
-
1．如图，Rt△A′BC′≌Rt△ABC，∠ACB=∠A′C′B=90°，△A′BC′绕点B顺时针方向旋转，AA′，CC′相交于点E．
（1）当∠CBC′=90°时，线段AE与A′E的数量关系是：；
（2）当∠CBC′≠90°时，（1）的结论是否成立？若成立，请结合图2说明理由；
（3）若BC=5，AC=3，当AC′∥BC时，请直接写出CC′的长．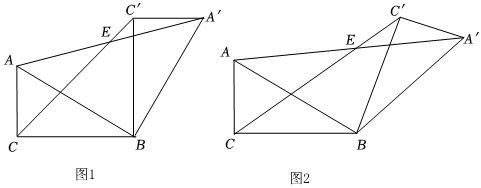
发布：2025/5/24 17:0:2组卷：48引用：1难度：0.1 -
2．观察猜想
（1）如图1，在等边△ABC与等边△ADE中，△ADE绕点A顺时针旋转α度（0＜α＜360），则线段BD与线段CE的数量关系是 ，直线BD与直线CE相交所成较小角的度数是 ；
类比探究
（2）如图2，在△ABC与△ADE中，∠BCA=∠DEA=90°，CB=CA，ED=EA，其他条件不变，（1）中的两个结论是否成立？若成立，请说明理由；若不成立，请写出新的结论并证明；
拓展应用
（3）如图3，在△ABC与△ADE中，∠ABC=∠ADE=90°，∠BAC=∠DAE=60°，AB=3AD=3，当B，D，E三点共线时，直接写出CE的值．3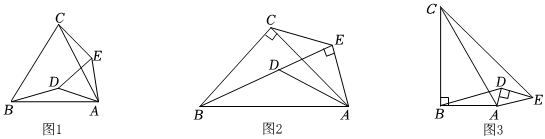
发布：2025/5/24 20:0:2组卷：208引用：1难度：0.1 -
3．如图1，△ABC中，∠ABC=45°，AH⊥BC于点H，点D在AH上，且DH=CH，连结BD．
（1）求证：BD=AC；
（2）将△BHD绕点H旋转，得到△EHF（点B，D分别与点E，F对应），连接AE．
①如图2，当点F落在AC上时（F不与C重合），若CF=1，tanC=3，求AE的长；
②如图3，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的数量关系，并说明理由．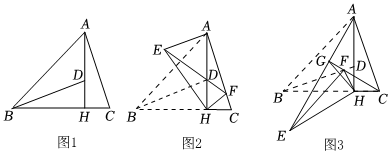
发布：2025/5/24 20:30:2组卷：60引用：1难度：0.1
