在数学课本第12章《整式乘除》里学习了两数和的平方公式，还记得它是如何被发现的吗？
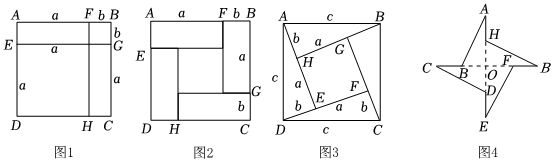
如图1的面积，把图1看作一个大正方形，它的面积是（a+b）²，如果把图1看作是由2个长方形和2个小正方形组成的，它的面积为a²+2ab+b²，由此得到：（a+b）²=a²+2ab+b²．
类比探究一：
（1）如图2，正方形ABCD是由四个边长分别是a,b的长方形和中间一个小正方形组成的，用不同的法对图2的面积进行计算，你发现的等式是

（a+b）²-4ab=（a-b）²

（a+b）²-4ab=（a-b）²

（用a,b表示）；
类比探究二：
（2）如图3，正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的，对图3的面积进行计算，你发现的式子是

c²=a²+b²

c²=a²+b²

（用a,b,c表示，结果化为最简）；
应用探索结果解决问题：
（3）如图3，正方形ABCD的边长是c,它由四个直角边长分别是a,b的角三角形和中间一个小正方形组成的，当c=5，a-b=1时，求a+b的值．
（4）如图4，将四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为80，OA=12．则该图形的面积为

120

120

．