 安阳某数学小组就“演绎推理是研究图形属性的重要方法”进行了学习,请你一起完成如下任务:
安阳某数学小组就“演绎推理是研究图形属性的重要方法”进行了学习,请你一起完成如下任务:
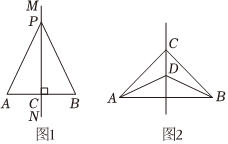
引入:我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,如图1,直线MN是线段AB的垂直平分线,P是MN上任意一点,连接PA、PB,将线段AB沿直线MN对折(或对称),我们发现PA与PB完全重合,由此即有:线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等.
| 任务一:请你根据“引入”,结合图形把已知和求证补充完整,并写出证明过程. 已知:如图1,MN⊥AB,垂足为C, AC=BC AC=BC .点P是直线MN上的任意一点.求证: PA=PB PA=PB ;证明: ∵MN⊥AB, ∴∠PCA=∠PCB=90°, 在△PCA和△PCB中,
∴△PCA≌△PCB(SAS), ∴PA=PB ∵MN⊥AB, ;∴∠PCA=∠PCB=90°, 在△PCA和△PCB中,
∴△PCA≌△PCB(SAS), ∴PA=PB |
如图2,CD是线段AB的垂直平分线,则∠CAD与∠CBD有何关系?请说明理由.
【答案】AC=BC;PA=PB;∵MN⊥AB,
∴∠PCA=∠PCB=90°,
在△PCA和△PCB中,
,
∴△PCA≌△PCB(SAS),
∴PA=PB
∴∠PCA=∠PCB=90°,
在△PCA和△PCB中,
AC = BC |
∠ PCA =∠ PCB |
PC = PC |
∴△PCA≌△PCB(SAS),
∴PA=PB
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/31 18:0:8组卷:36引用:4难度:0.7
相似题
-
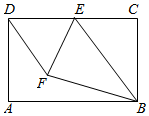 1.如图,在矩形ABCD中,AB=3,BC=2,点E为CD的中点.将△BCE沿BE折叠,使点C落在矩形内的点F处,连接DF,则DF的长为( )发布:2025/6/18 3:30:2组卷:442引用:1难度:0.5
1.如图,在矩形ABCD中,AB=3,BC=2,点E为CD的中点.将△BCE沿BE折叠,使点C落在矩形内的点F处,连接DF,则DF的长为( )发布:2025/6/18 3:30:2组卷:442引用:1难度:0.5 -
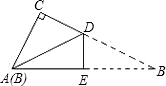 2.一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°,AC=,则折痕DE的长等于3.发布:2025/6/18 6:0:1组卷:344引用:11难度:0.5
2.一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°,AC=,则折痕DE的长等于3.发布:2025/6/18 6:0:1组卷:344引用:11难度:0.5 -
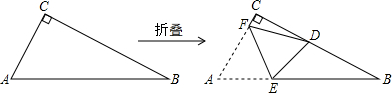
3.直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、点F.探究:如果折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.
 发布:2025/6/18 2:0:1组卷:380引用:6难度:0.1
发布:2025/6/18 2:0:1组卷:380引用:6难度:0.1


