量化分析是解决数学问题的重要策略．在初中几何学习的历程中，借助量化去分析图形特征往往更能直击问题本质，是一种大道至简的思路．
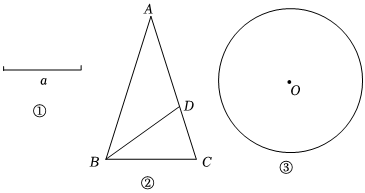
【量化构形】
（1）如图①，已知线段a,用无刻度直尺和圆规求作线段b,使得b=5a；（不写作法，保留作图痕迹）
【量化解数】
顶角为36°的等腰三角形称为“锐角黄金三角形”．
（2）如图②，△ABC和△BCD都是锐角黄金三角形．求证：CD=5-12⋅BC；
【量化作图】
（3）如图③，已知⊙O，用无刻度直尺和圆规作⊙O的内接“锐角黄金三角形”．（保留作图痕迹，并写出必要的文字说明）
b
=
5
a
CD
=
5
-
1
2
⋅
BC
【考点】圆的综合题．
【答案】（1）见解析；（2）见解析；（3）见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/18 9:0:1组卷：110引用：2难度：0.5
相似题
-
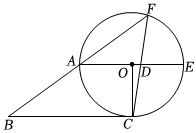1．如图，四边形OABC中，AO∥BC，∠AOC=90°，AO=3，AB=5．以O为圆心，OA为半径作圆，⊙O经过点C，且与BA的延长线交于F．延长AO交圆于E，连接FC交AE于点D．
（1）求证：BC是⊙O的切线；
（2）求cos∠FAE的值；
（3）求线段OD的长．发布：2025/6/7 5:0:1组卷：79引用：1难度：0.3 -
2．等腰三角形AFG中AF=AG，且内接于圆O，D、E为边FG上两点（D在F、E之间），分别延长AD、AE交圆O于B、C两点（如图1），记∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）连接CF，交AB于H（如图2）．若β=45°，且BC×EF=AE×CF．求证：∠AHC=2∠BAC；
（3）在（2）的条件下，取CH中点M，连接OM、GM（如图3），若∠OGM=2α-45°，
①求证：GM∥BC，GM=BC；12
②请直接写出的值．OMMC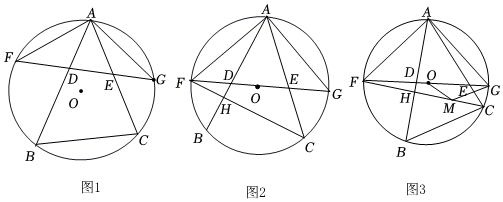
发布：2025/6/7 16:0:2组卷：1490引用：8难度：0.1 -
3．已知，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是优弧CBD上的任意一点，AH=2，CH=4．
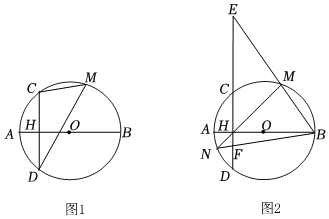
（1）如图1，
①求⊙O的半径；
②求sin∠CMD的值．
（2）如图2，直线BM交直线CD于点E，直线MH交⊙O于点N，连结BN交CD于点F，求HE•FH的值．发布：2025/6/7 7:0:1组卷：476引用：2难度：0.3
