阅读与思考
下面是一位同学的数学学习笔记，请仔细阅读并完成相应任务，
| 瓦里尼翁平行四边形 我们知道，如图1，在四边形ABCD中，点E、F、G，H分别是边AB、BC，CD，DA的中点，顺次连接E，F、G、H，得到的四边形EFGH是平行四边形． 我查阅了许多资料，得知这个平行四边形EFGH被称为瓦里尼翁平行四边形．瓦里尼翁（Varingnon,Pierte1654-1722）是法国数学家、力学家．瓦里尼翁平行四边形与原四边形关系密切． ①当原四边形的对角线满足一定关系时，瓦里尼翁平行四边形可能是菱形、矩形或正方形． ②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系． ③瓦里尼翁平行四边形的面积等于原四边形面积的一半．此结论可借助图1证明如下： 证明：如图2，连接AC，分别交EH，FG于点P、Q，过点D作DM⊥AC于点M，交HG于点N． ∵H、G分别为AD，CD的中点，∴HG∥AC，HG= 1 2 ∴ DN NM = DG GC 1 2 ∵四边形EFGH是瓦里尼翁平行四边形， ∴HE∥GF，即HP∥GQ． ∵HG∥AC，即HG∥PQ， ∴四边形HPQG是平行四边形，（依据2）． ∴S▱HPQG=HG•MN= 1 2 ∵S△ADC= 1 2 1 2 S △ ADC  |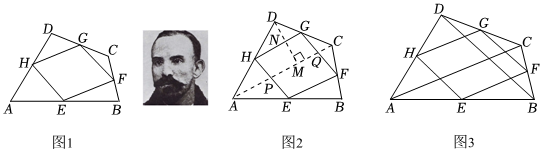
三角形中位线定理
三角形中位线定理
；依据2是指：
两组对边分别平行的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
；（2）如图，方格纸中每个小正方形的边长均为1，画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH，满足下列要求①四边形ABCD及它的瓦里尼翁平行四边形EFGH的顶点都在小正方形网格的格点的上；②四边形EFGH是矩形，不是正方形；
（3）在图1中，分别连接AC，BD得到图3，请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC、BD长度的关系，并证明你的结论．
【考点】相似形综合题．
【答案】三角形中位线定理；两组对边分别平行的四边形是平行四边形
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/4 8:0:9组卷：134引用：2难度：0.5
相似题
-
1．在矩形ABCD中，AD=3，CD=4，点E在边CD上，且DE=1．
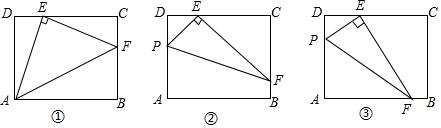
感知：如图①，连接AE，过点E作EF⊥AE，交BC于点F，连接AF，易证：△ADE≌△ECF（不需要证明）；
探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE∽△ECF；
应用：如图③，若EF交AB边于点F，其他条件不变，且△PEF的面积是3，则AP的长为．发布：2025/6/16 19:30:1组卷：681引用：3难度：0.1 -
2．如图，已知直线l1∥l2，线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．
（1）求证：△ABP≌△CBE；
（2）连接AD、BD，BD与AP相交于点F．如图2．
①当=2时，求证：AP⊥BD；BCBP
②当=n（n＞1）时，设△PAD的面积为S1，△PCE的面积为S2，求BCBP的值．S1S2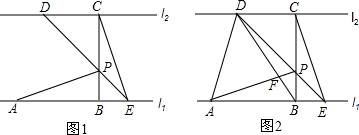
发布：2025/6/18 11:30:2组卷：1185引用：6难度：0.3 -
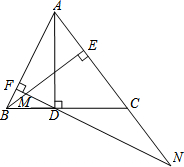3．如图，AD、BE是△ABC的两条高，过点D作DF⊥AB，垂足为F，FD交BE于M，FD、AC的延长线交于点N．
（1）求证：△BFM∽△NFA；
（2）试探究线段FM、DF、FN之间的数量关系，并证明你的结论；
（3）若AC=BC，DN=12，ME：EN=1：2，求线段AC的长．发布：2025/6/16 11:30:2组卷：851引用：7难度：0.3
