学习了《四边形》后，刘老师设置了一个问题情境，供同学们讨论．
问题情境：正方形ABCD中，点P为边AB上一个动点，连接CP，过点C作CQ⊥CP交射线AD于点Q，连接PQ，点E为PQ的中点，连接DE．
讨论△CPQ的性质及AP与DE的数量关系．
以下是同学们的讨论过程，请仔细阅读并完成任务：
| 小明：我得出△CPQ是等腰直角三角形， 理由：∵四边形ABCD是正方形， ∴CD=BC，∠DCB=∠CDA=∠BAD=∠CBA=90°，DA=BA， 又CQ⊥CP， ∴∠QCP=90°， ∴∠QCD=∠PCB=90°-∠DCP，∠CDQ=180°-90°=90°， ∴∠CDQ=∠CBP， ∴△CDQ≌△CBP ∴CQ=CP，∴△CPQ是等腰直角三角形； 小亮：没能求出AP与DE的数量关系，但我感觉过P作PG∥DE交DA于G后可以求出． |
任务：
（1）小明的理由中，△CDQ≌△CBP的依据是
④
④
；（填序号）．①SSS ②SAS ③AAS ④ASA ⑤HL
（2）请根据小亮的提示判断AP与DE的数量关系，并说明理由；
（3）当点P在射线AB上运动时，若AB=3，DQ=1，直接写出DE的长．
【考点】四边形综合题．
【答案】④
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/8 8:0:8组卷：50引用：2难度：0.5
相似题
-
1．如图1，菱形ABCD中，∠A=120°，AB=4，点P在CD上，连接BP，将△BCP沿BP翻折，得到△BMP，连接CM，延长CM交AD于点E．
（1）当点P从点C运动到点D时，AE的长随之变化，请写出AE长的取值范围：．
（2）在图2中，当MP⊥CD时，求证：BM平分∠ABC．
（3）当点P在CD上移动过程中，是否存在CP=AE的情况？如果存在，求此时CP的长；如果不存在，说明理由．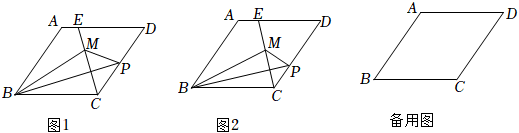
发布：2025/5/25 10:0:1组卷：79引用：1难度：0.1 -
2．【问题探究】
（1）如图①，在四边形ABCD中，∠B=∠D=90°，∠DAB=135°，且AB=2，AD=4．若点P是BC边上任意一点，且∠APD=45°，求BP的长；2
【问题解决】
（2）如图②，直角△ABC是一个公园的平面示意图，∠B=90°，∠A=60°，AB=200m,为了人们能更好的放松娱乐，现要扩大公园使其成为一个四边形ABCD，根据设计要求，需使△ACD为等腰三角形，且AC=BD，是否可以建一个满足要求的面积最大的四边形公园ABCD？若可以，求出满足要求的四边形ABCD的最大面积；若不可以，请说明理由．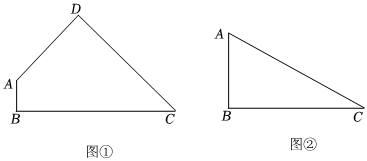
发布：2025/5/25 10:30:1组卷：46引用：1难度：0.3 -
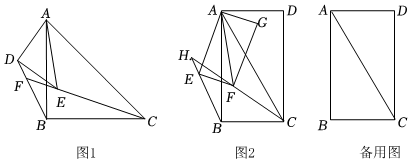3．（1）问题发现
如图1，在等腰直角三角形ABC和等腰直角三角形ADE中，∠ABC=∠ADE=90°，连接BD，交CE的延长线于点F．
填空：的值为 ，∠BFC的度数为 ．CEBD
（2）类比探究
如图2，在矩形ABCD和矩形AEFG中，∠BAC=∠EAF=30°，连接BE，CF，BE的延长线和CF的延长线交于点H．请求出的值及∠BHC的度数．BECF
（3）拓展延伸
在（2）的条件下，将矩形AEFG绕点A在平面内自由旋转，BE，CF所在直线交于点H．若AB=，请直接写出BH的最大值．3发布：2025/5/25 11:0:2组卷：684引用：3难度：0.3
