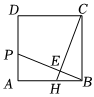
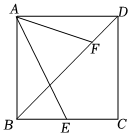
在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．
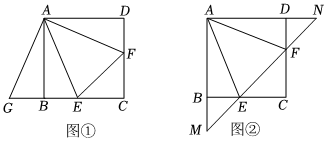
（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；
（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/29 20:0:2组卷：1653引用：6难度：0.3
相似题
-
1．如图，在正方形ABCD中，点H是AD的中点，点P是对角线BD上的一点（不与端点重合），过P作PE⊥BC于E，PF⊥CD于F，连接EF，PH，若AB=2，则PH+EF的最小值为 ．发布：2025/6/9 14:30:1组卷：315引用：2难度：0.5 -
2．如图，正方形ABCD的边长为4，对角线AC，BD相交于点O，点E，F分别在BC，CD的延长线上，且CE=2，DF=1，G为EF的中点，连接OE，交CD于点H，连接GH，则GH的长为 ．发布：2025/6/9 15:0:1组卷：5152引用：22难度：0.6 -
3．如图，正方形ABCD中，AB=12，点E，F分别为AD，BC上一点，且AE=BF=7，连接EF交对角线BD于点G，点P，Q分别为CE，BG的中点，则PQ的长为（ ）发布：2025/6/9 15:0:1组卷：879引用：4难度：0.6
