求代数式x2-4x+3的最小值时，我们通常运用“a2≥0”．这个公式对代数式进行配方来解决．比如x2-4x+3=x2-4x+4-1=（x-2）2-1，∵（x-2）2≥0，∴（x-2）2-1≥-1，∴x2-4x+3的最小值是-1，试利用“配方法”解决下列问题：
（1）填空：x2+6x+13=（x+33）2+44；
（2）求x2+y2+2x-4y+10的最小值；
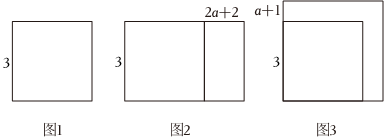
（3）如图，将边长为3的正方形一边保持不变，另一组对边增加2a+2（a＞0）得到如图2所示的新长方形，此长方形的面积为S1将正方形的边长增加a+1（a＞0），得到如图3所示的新正方形，此正方形的面积为S2．
①用含a的代数式表示出S1，S2；
②比较S1，S2的大小．
【考点】配方法的应用；非负数的性质：偶次方．
【答案】3；4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/8 13:0:8组卷：78引用：1难度：0.5
