（1）问题发现：如图①，直线AB∥CD，E是AB与CD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．
请把下面的证明过程补充完整：
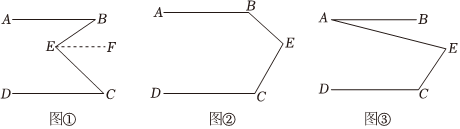
证明：过点E作EF∥AB，
∵AB∥CD（已知），EF∥AB（已作），
∴EF∥CD（ 平行于同一条直线的两直线平行平行于同一条直线的两直线平行）．
∴∠C=∠CEF（ 两直线平行，内错角相等两直线平行，内错角相等）．
∵EF∥AB，
∴∠B=∠BEF∠BEF（ 两直线平行，内错角相等两直线平行，内错角相等），
∵∠CEF+∠BEF=∠BEC，
∴∠B+∠C=∠BEC（等量代换）．
（2）拓展探究：如果点E运动到图②所示的位置，其他条件不变，进一步探究发现：∠B，∠C，∠BEC之间的关系是 ∠B+∠C+∠BEC=360°∠B+∠C+∠BEC=360°；
（3）解决问题：如图③，AB∥DC，∠C=120°，∠AEC=80°，请求出∠A的度数．
【考点】平行线的判定与性质．
【答案】平行于同一条直线的两直线平行；两直线平行，内错角相等；∠BEF；两直线平行，内错角相等；∠B+∠C+∠BEC=360°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/25 8:0:9组卷：73引用：2难度：0.5
相似题
-
1．如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：
①BC平分∠ABE；
②AC∥BE；
③∠CBE+∠EDB=90°；
④∠DEB=2∠ABC，其中正确的有（ ）发布：2025/6/15 23:0:1组卷：1639引用：9难度：0.5 -
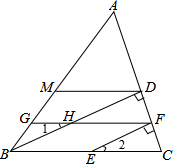2．已知BD⊥AC于点D，EF⊥AC于点F，∠AMD=∠AGF，∠1=∠2=28°．
（1）求∠GFC的度数；
（2）求证：DM∥BC．发布：2025/6/15 23:0:1组卷：482引用：4难度：0.6 -
3．下列说法中正确的个数有（ ）
（1）若a∥b,b∥c,则a∥c.（2）在同一平面内，不相交的两条线段必平行．（3）相等的角是对顶角．（4）两条直线被第三条直线所截，所得到同位角相等．（5）若a⊥b,b⊥c,则a⊥c.（6）两条平行线被第三条直线所截，一对内错角的角平分线互相平行．发布：2025/6/15 23:0:1组卷：1418引用：3难度：0.7
