结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示5和2的两点之间的距离是 33；表示-3和2两点之间的距离是 55；一般地，数轴上表示数m和数n的两点之间的距离等于|m-n|．如果表示数a和-2的两点之间的距离是3，那么a=1或-51或-5．
（2）若数轴上表示数a的点位于-4与2之间，则|a+4|+|a-2|的值为 66．
（3）利用数轴找出所有符合条件的整数点x,使得|x+2|+|x-5|=7，这些点表示的数的和是 1212．
（4）当a=11时，|a+3|+|a-1|+|a-4|的值最小，最小值是 77．
【答案】3；5；1或-5；6；12；1；7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 16:0:8组卷：413引用：2难度：0.6
相似题
-
1．数轴上，表示-4与2的点之间的距离是2-（-4）=6，表示-4与-1的点之间的距离是-1-（-4）=3，即数轴上两点之间的距离等于较大数与较小数的差，若不知道数轴上两数的大小，则表示数m与n的点之间的距离可以表示为|m-n|，利用上述结论解决如下问题．
若|x-5|=3，求x的值．发布：2025/6/8 2:30:2组卷：9引用：3难度：0.8 -
2．在数轴上A、B两点表示的数分别是-2和4，在数轴上有另外一点P，点P到A、B两点的距离和是10，则点P表示的数是 ．
发布：2025/6/7 23:30:2组卷：26引用：2难度：0.7 -
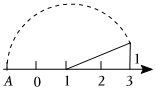3．如图所示，在数轴上点A所表示的数为a,则a的值为 ．发布：2025/6/8 1:30:1组卷：239引用：16难度：0.7
