某商店为了推销一种新产品，在某地先后举行40场产品发布会，已知该产品每台成本为10万元，设第x场
产品的销售量为y（台），已知第一场销售产品49台，然后每增加一场，产品就少卖出1台；
（1）直接写出y与x之间满足的函数关系式；
产品的每场销售单价p（万元）由基本价和浮动价两部分相加组成，其中基本价保持不变．经过统计，发现第1场一第20场浮动价与发布场次x成正比，第21场一一第40场浮动价与发布场次x成反比，得到如下数据：
| x（场） | 3 | 10 | 25 |
| P（万元） | 10.6 | 12 | 14.2 |
（3）当产品销售单价为13万元时，求销售场次是第几场？
（4）在这40场产品发布会中，求哪一场获得的利润最大，最大利润是多少？
【答案】（1）y=50-x；
（2）当1≤x≤20且x为正整数时，P与x之间满足的函数关系式为p=0.2x+10；当21≤x≤40且x为正整数时，P与x之间满足的函数关系式为P=+10；
（3）当产品销售单价为13万元时，销售场次是第15场和第35场；
（4）第21场获得的利润最大，最大利润为145万元．
（2）当1≤x≤20且x为正整数时，P与x之间满足的函数关系式为p=0.2x+10；当21≤x≤40且x为正整数时，P与x之间满足的函数关系式为P=
105
x
（3）当产品销售单价为13万元时，销售场次是第15场和第35场；
（4）第21场获得的利润最大，最大利润为145万元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/13 8:0:8组卷：650引用：2难度：0.3
相似题
-
1．某商场出售一批进价为2元的贺卡，在市场营销中发现，此商品的日销售单价x（单位：元）与日销售数量y（单位：张）之间有如下关系：
（1）根据表中数据在平面直角坐标系中描出实数对（x,y）的对应点；销售单价x（元） 3 4 5 6 日销售量y（张） 20 15 12 10
（2）确定y与x之间的函数关系式，并画出图象；
（3）设销售此贺卡的日纯利润为w元，试求出w与x之间的函数关系式．若物价局规定该贺卡售价最高不超过10元/张，请你求出日销售单价x定为多少元时，才能获得最大日销售利润？发布：2025/6/17 21:0:1组卷：627引用：35难度：0.3 -
2．某药品研究所研发一种抗菌新药，测得成人服用该药后血液中的药物浓度（微克/毫升）与服药后时间x（小时）之间的函数关系如图所示，当血液中药物浓度上升（0≤x≤a）时，满足y=2x,下降时，y与x成反比．
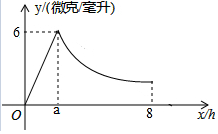
（1）求a的值，并求当a≤x≤8时，y与x的函数表达式；
（2）若血液中药物浓度不低于3微克/毫升的持续时间超过4小时，则称药物治疗有效，请问研发的这种抗菌新药可以作为有效药物投入生产吗？为什么？发布：2025/6/17 21:30:1组卷：823引用：5难度：0.6 -
3．去学校食堂就餐，经常会在一个买菜窗口前等待．经调查发现，同学的舒适度指数y与等待
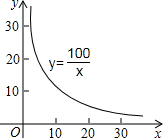时间x（分）之间存在如下的关系：y=，求：100x
（1）若等待时间x=5分钟时，求舒适度y的值；
（2）舒适度指数不低于10时，同学才会感到舒适．函数y=的图象如图（x＞0），请根据图象说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？100x发布：2025/6/18 6:0:1组卷：1118引用：11难度：0.5
