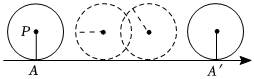
【操作感知】如图1，长方形透明纸上有一条数轴，AB是周长为4的圆的直径，点A与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点A落在数轴上的点A'处；将圆从原点出发沿数轴负方向滚动半周，点B落在数轴上的点B′处，折叠长方形透明纸，使数轴上的点A′与点B′重合，此时折痕与数轴交点表示的数为

1

1

．
【建立模型】折叠长方形透明纸，使得数轴上表示数a的点C与表示数b的点D重合，则折痕与数轴交点表示的数为

a

+

b

2

a

+

b

2

．（用含a,b的代数式表示）
【问题解决】如图2，点P表示的数为-10，点Q表示的数为20，如果点M从点P的位置出发，以每秒2个单位的速度向点Q运动，当点M到达点Q时停止运动，设运动时间为t秒（t＞0）．
（1）若点M到P，Q两点中一点的距离为到另一点距离的两倍，求t值．
（2）若点M从点P出发，同时点N从点Q开始运动，以每秒1个单位的速度向点P运动，并与点M同时停止，请求出当点M，N，P中其中一点到另外两点距离相等时t的值．