已知函数y=-12x2+x+12（x≥a） 12x2+x-12（x＜a）
（a为常数）．
（1）当a=0时，
①若点P（3，m）在此函数图象上，则m的值为 -1-1；
②若点Q（n,14）在此函数图象上，求n的值；
③当此函数图象与直线y=b有三个交点时，直接写出b的取值范围 12≤b＜1或-1＜b＜-1212≤b＜1或-1＜b＜-12；
（2）已知A（-2，a），B（-2，-a），C（3，-a），D（3，a），当函数图象与四边形ABCD的边有3个公共点时，直接写出a的取值范围．
y
=
- 1 2 x 2 + x + 1 2 （ x ≥ a ） |
1 2 x 2 + x - 1 2 （ x ＜ a ） |
Q
（
n
,
1
4
）
1
2
≤
b
＜
1
-
1
＜
b
＜
-
1
2
1
2
≤
b
＜
1
-
1
＜
b
＜
-
1
2
【考点】四边形综合题．
【答案】-1；或
1
2
≤
b
＜
1
-
1
＜
b
＜
-
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/18 3:0:1组卷：20引用：2难度：0.5
相似题
-
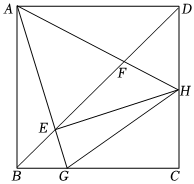1．如图，在正方形ABCD中，点G为BC边上的动点，点H为CD边上的动点，且满足BG+DH=HG，连接AH，AG分别交正方形ABCD的对角线BD于F，E两点，则下列结论中正确的有 .（填序号即可）
①∠DHA=∠GHA；②AF•AH=AE•AG；③BE+DF=EF；④AH=AE2发布：2025/5/24 5:30:2组卷：250引用：1难度：0.3 -
2．如图1，在矩形ABCD中，AB=3，AD=4．P为对角线BD上的点，过点P作PM⊥AD于点M，PN⊥BD交BC于点N，Q是M关于PD的对称点，连结PQ，QN．
（1）如图2，当Q落在BC上时，求证：BQ=MD．
（2）是否存在△PNQ为等腰三角形的情况？若存在，求MP的长；若不存在，请说明理由．
（3）若射线MQ交射线DC于点F，当PQ⊥QN时，求DF：FC的值．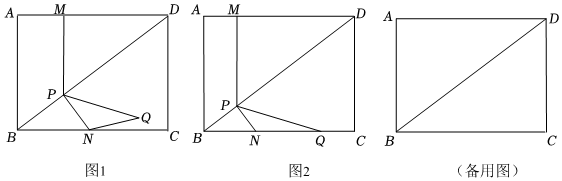
发布：2025/5/24 6:0:2组卷：366引用：3难度：0.1 -
3．四边形ABCD为正方形，AB=8，点E为直线BC上一点，射线AE交对角线BD于点F，交直线CD于点G．
（1）如图，点E在BC延长线上．求证：△CFG∽△EFC；
（2）是否存在点E，使得△CFG是等腰三角形？若存在，求BE的长；若不存在，请说明理由．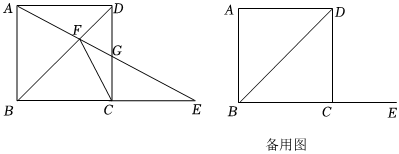
发布：2025/5/24 7:0:1组卷：57引用：1难度：0.1
