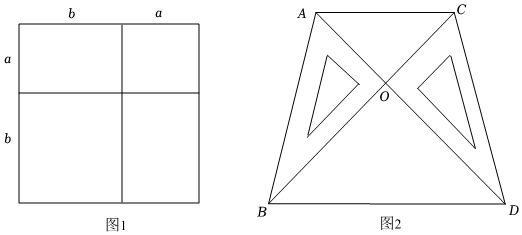
【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到（a+b）2=a2+2ab+b2基于此，请解答下列问题：
【直接应用】（1）若x+y=3，x2+y2=5，求xy的值；
【类比应用】（2）①若（x-3）（x-4）=1，则（x-3）2+（x-4）2=33；
②若x满足（3-4x）（2x-5）=92，求（3-4x）2+4（2x-5）2的值；
③若x满足（2023-x）2+（2020-x）2=2023，求（2023-x）（2020-x）的值；
【知识迁移】（3）两块全等的特制直角三角板（∠AOB=∠COD=90°）如图2所示放置，其中A，O，D在一直线上，连接AC，BD．若AD=16，S△AOC+S△BOD=68，求一块直角三角板的面积．
（
3
-
4
x
）
（
2
x
-
5
）
=
9
2
【答案】3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/9 6:0:3组卷：214引用：1难度：0.4
相似题
-
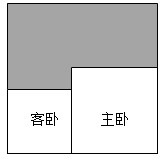1．如图所示的是正方形的房屋结构平面图，其中主卧与客卧都是正方形，其面积之和比其余面积（阴影部分）多6.25m2，则主卧与客卧的周长差是（ ）发布：2025/1/1 6:30:3组卷：212引用：4难度：0.6 -
2．灵活运用完全平方公式（a±b）2=a2±2ab+b2可以解决许多数学问题．
例如：已知a-b=3，ab=1，求a2+b2的值．
解：∵a-b=3，ab=1，∴（a-b）2=9，2ab=2，∴a2-2ab+b2=9，∴a2-2+b2=9，∴a2+b2=9+2=11．
请根据以上材料，解答下列问题．
（1）若a2+b2与2ab-4互为相反数，求a+b的值．
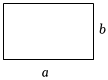
（2）如图，矩形的长为a,宽为b,周长为14，面积为8，求a2+b2的值．发布：2025/5/23 21:0:1组卷：435引用：4难度：0.6 -
3．如图，一个正方形被分成两个正方形和两个一模一样的矩形，请根据图形，写出一个含有a,b的正确的等式．发布：2025/5/25 0:30:1组卷：573引用：8难度：0.5
