如图1,∠ACD是△ABC的外角,∠ABC与∠ACD的角平分线交于点O.
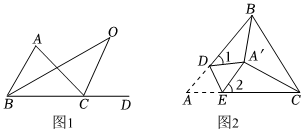
(1)若∠ABC=66°,∠ACB=34°,则∠A=8080°,∠O=4040°;
(2)探索∠A与∠O的数量关系,并说明理由;
(3)若AB∥CO,AC⊥BO,求∠ACB的度数;
(4)如图2,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为 120°120°.
【考点】平行线的性质.
【答案】80;40;120°
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/11 5:0:1组卷:125引用:3难度:0.5