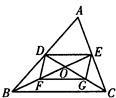
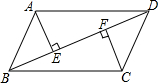
如图，在△ABC中，∠BAC=90°，∠B=45°，BC=10，过点A作AD∥BC，且点D在点A的右侧．点P从点A出发沿射线AD方向以每秒1个单位的速度运动，同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动，在线段QC上取点E，使得QE=2，连接PE，设点P的运动时间为t秒．
（1）若PE⊥BC，求BQ的长；
（2）请问是否存在t的值，使以A，B，E，P为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由．
【考点】平行四边形的判定．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：9745引用：21难度：0.3
