【深度阅读】苏格兰哲学家托马斯•卡莱尔（1795-1881）曾给出了一元二次方程x2+bx+c=0的几何解法：如图1，在平面直角坐标系中，已知点A（0，1），B（-b,c），以AB为直径作⊙P．若⊙P交x轴于点M（m,0），N（n,0），则m,n为方程x2+bx+c=0的两个实数根．
【自主探究】（1）由勾股定理得，AM2=12+m2，BM2=c2+（-b-m）2，AB2=（1-c）2+b2，在Rt△ABM中，AM2+BM2=AB2，所以12+m2+c2+（-b-m）2=（1-c）2+b2．化简得：m2+bm+c=0．同理可得：n2+bn+c=0n2+bn+c=0．
所以m,n为方程x2+bx+c=0的两个实数根．
【迁移运用】（2）在图2中的x轴上画出以方程x2-3x-2=0两根为横坐标的点M，N．
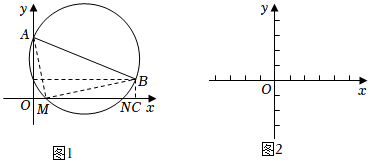
（3）已知点A（0，1），B（4，-3），以AB为直径作⊙C．判断⊙C与x轴的位置关系，并说明理由．
【拓展延伸】（4）在平面直角坐标系中，已知两点A（0，a），B（-b,c），若以AB为直径的圆与x轴有两个交点M，N，则以点M，N的横坐标为根的一元二次方程是 x2+bx+ac=0x2+bx+ac=0．
【考点】圆的综合题．
【答案】n2+bn+c=0；x2+bx+ac=0
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/11 1:0:1组卷：134引用：2难度：0.4
相似题
-
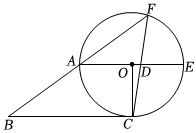1．如图，四边形OABC中，AO∥BC，∠AOC=90°，AO=3，AB=5．以O为圆心，OA为半径作圆，⊙O经过点C，且与BA的延长线交于F．延长AO交圆于E，连接FC交AE于点D．
（1）求证：BC是⊙O的切线；
（2）求cos∠FAE的值；
（3）求线段OD的长．发布：2025/6/7 5:0:1组卷：79引用：1难度：0.3 -
2．等腰三角形AFG中AF=AG，且内接于圆O，D、E为边FG上两点（D在F、E之间），分别延长AD、AE交圆O于B、C两点（如图1），记∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）连接CF，交AB于H（如图2）．若β=45°，且BC×EF=AE×CF．求证：∠AHC=2∠BAC；
（3）在（2）的条件下，取CH中点M，连接OM、GM（如图3），若∠OGM=2α-45°，
①求证：GM∥BC，GM=BC；12
②请直接写出的值．OMMC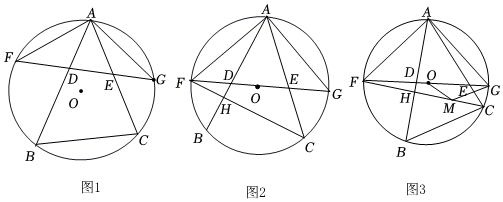
发布：2025/6/7 16:0:2组卷：1490引用：8难度：0.1 -
3．已知，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是优弧CBD上的任意一点，AH=2，CH=4．
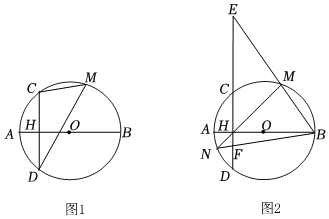
（1）如图1，
①求⊙O的半径；
②求sin∠CMD的值．
（2）如图2，直线BM交直线CD于点E，直线MH交⊙O于点N，连结BN交CD于点F，求HE•FH的值．发布：2025/6/7 7:0:1组卷：476引用：2难度：0.3
