【问题原型】如图，在▱ABCD中，对角线AC的垂直平分线EF交AD于点F，交BC于点E，交AC于点O，连接AE，CF．求证：四边形AECF是菱形．
【甲同学的证法】证明：∵EF垂直平分AC，
∴OA=OC，（第一步）
∵OE=OF，（第二步）
∴四边形AECF是平行四边形，（第三步）
又∵EF⊥AC，（第四步）
∴四边形AECF是菱形．（第五步）
【老师评析】甲同学想先利用对角线互相平分证明四边形AECF是平行四边形，再利用对角线互相垂直证明它是菱形，可惜有一步错了．
【挑错改错】
（1）甲同学的证明过程在第 二二步出现了错误；
（2）请你根据甲同学的证明思路写出此题正确的证明过程；
（3）直接写出当△ABC中的∠ACB=45°45°时，四边形AECF是正方形．
【考点】四边形综合题．
【答案】二；45°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：39引用：2难度：0.5
相似题
-
1．如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．
（1）若∠B=60°，这时点P与点C重合，则∠NMP=度；
（2）求证：NM=NP；
（3）当△NPC为等腰三角形时，求∠B的度数．
发布：2025/6/19 1:30:1组卷：2881引用：6难度：0.5 -
2．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：．
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，探求AH满足的数量关系．（可利用（2）得到的结论）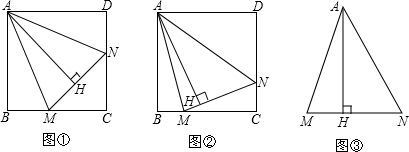
发布：2025/6/17 11:30:1组卷：879引用：1难度：0.3 -
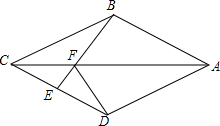3．如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．
（1）证明：∠BAC=∠DAC，∠AFD=∠CFE；
（2）若AB∥CD，试证明四边形ABCD是菱形；
（3）在（2）的条件下，若BE⊥CD，试证明∠EFD=∠BCD．发布：2025/6/18 8:30:2组卷：215引用：3难度：0.1
