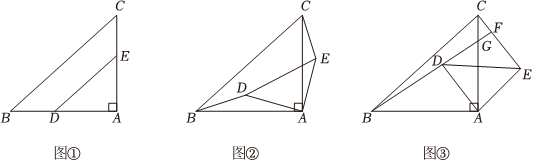
如图①,在△ABC中,∠A=90°,AB=AC,点D、E分别在边AB、AC上(点D不与点A、B重合),且AD=AE.连接DE.
问题原型:将图①中△ADE绕点A顺时针旋转α(0°<α<90°),如图②.求证:△ABD≌△ACE;
初步探究:在问题原型的条件下,延长BD交直线AC于点G,交直线CE于点F,请利用图③探究BD与CE的关系,并说明理由;
简单应用:如图③,把图①中的△ADE绕点A顺时针旋转α°(0<α<90),连结BD和CE,延长BD交CE于点F.若∠FDE=52°,则∠FED=3838°.
【考点】全等三角形的判定与性质;旋转的性质.
【答案】38
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/27 8:0:2组卷:165引用:7难度:0.4