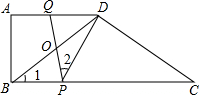
如图，在四边形ABCD中，AD∥BC，∠A=90°，BD=DC，AB=6，AD=8，点P、Q分别为BC、AD上的动点，连接PQ，与BD相交于点O，
（1）当∠1=∠2时，求证：∠DOQ=∠DPC；
（2）在（1）的条件下，求证：DQ•PC=BD•DO；
（3）如果点P由点B向点C移动，每秒移动2个单位，同时点Q由点D向点A移动，每秒移动1个单位，设移动的时间为t秒，是否存在某以时刻，使得△BOP为直角三角形？如果存在，请求出t的值；如果不存在，请说明理由．
【考点】相似形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 5:0:10组卷：625引用：4难度：0.1
相似题
-
1．已知：如图，正方形ABCD与正方形AEFG．
（1）如图①，求证：BG=DE；
（2）如图②，求的值；CFBG
（3）如图③，分别取CF、BE的中点M、N，试探究：MN与BE的关系，并说明理由．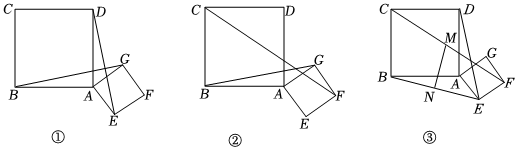
发布：2025/6/9 16:30:1组卷：218引用：3难度：0.2 -
2．【初步探究】
（1）把矩形纸片ABCD如图①折叠，当点B的对应点B'在MN的中点时，填空：△EB'M △B'AN（“≌”或“∽”）．
【类比探究】
（2）如图②，当点B的对应点B'为MN上的任意一点时，请判断（1）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．
【问题解决】
（3）在矩形ABCD中，AB=4，BC=6，点E为BC中点，点P为线段AB上一个动点，连接EP，将△BPE沿PE折叠得到△B'PE，连接DE，DB'，当△EB'D为直角三角形时，BP的长为 ．
发布：2025/6/9 14:30:1组卷：832引用：9难度：0.2 -
3．已知AD是△ABC的中线，点E是线段AD上一点，过点E作AC的平行线，过点B作AD的平行线，两平行线交于点F，连结AF．
【方法感知】如图①，当点E与点D重合时，易证：△AEC≌△FBE．（不需证明）
【探究应用】如图②，当点E与点D不重合时，求证：四边形ACEF是平行四边形．
【拓展延伸】如图③，记AB与EF的交点为G，CE的延长线与AB的交点为N，且N为AB的中点．
（1）=；NGGA
（2）若CA⊥AB，BC=5时，则BF的长为 ．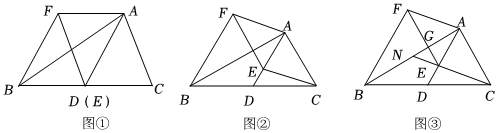
发布：2025/6/9 22:30:2组卷：252引用：5难度：0.3
