我们发现，“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题，这种方法称为等面积法．
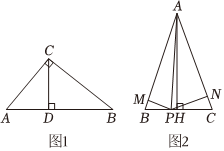
（1）如图1，BC是AC边上的高，CD是AB边上的高，我们知道S△=12×底×高，则S△ABC=12AC⋅BC=12AB•CD12AB•CD．
（2）如图1，若∠ACB=90°，AC=3，BC=4，AB=5，CD是斜边AB上的高线．用等面积法求CD的长．
（3）如图2，在等腰三角形ABC中，AB=AC=13，BC=10，过A作AH⊥BC于点H，且AH=12，P为底边BC上的任意一点，过点P作PM⊥AB，PN⊥AC，垂足分别为M，N，连接AP，利用S△ABC=S△ABP+S△ACP，求PM+PN的值．
1
2
S
△
ABC
=
1
2
AC
⋅
BC
1
2
1
2
【考点】面积及等积变换．
【答案】AB•CD
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 6:0:3组卷：225引用：1难度：0.3
相似题
-
1．如图，设一个三角形的三边分别是3，1-3m,8．
（1）求m的取值范围；
（2）是否存在整数m使三角形的周长为偶数？若存在，求出三角形的周长；若不存在，说明理由；
（3）如图，在（2）的条件下，当AB=8，AC=1-3m,BC=3时，若D是AB的中点，连CD，P是CD上动点（不与C，D重合，当P在线段CD上运动时，有两个式子）：①；②S△ABCS△APC+S△BPD，其中有一个的值不变，另一个的值改变．问题：PA+PBAB
A．请判断出谁不变，谁改变；
B．若不变的求出其值，若改变的求出变化的范围．发布：2024/11/1 8:0:2组卷：136引用：0难度：0.7 -
2．已知长方形的边长都是整数，将边长为2的正方形纸片放入长方形，要求正方形的边与长方形的边平行或重合，且任意两个正方形重叠部分的面积为0，放入的正方形越多越好．
（1）如果长方形的长是4，宽是3，那么最多可以放入多少个边长为2的正方形？长方形被覆盖的面积占整个长方形面积的百分比是多少？
（2）如果长方形的长是n（n≥4），宽是n-2，那么最多可以放入多少个边长为2的正方形？长方形被覆盖的面积占整个长方形面积的百分比是多少？
（3）对于任意满足条件的长方形，使长方形被覆盖的面积小于整个长方形面积的55%．求长方形边长的所有可能值．发布：2024/6/27 10:35:59组卷：68引用：1难度：0.5 -
3．如图所示，已知△ABC面积为1，点D、E、F分别在BC、CA、AB上，且BD=2DC，CE=2EA，AF=2FB，AD、BE、CF两两相交于P、Q、R，则△PQR的面积为（ ）发布：2024/12/8 14:0:3组卷：923引用：1难度：0.5
