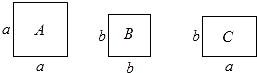
数形结合是一种重要的数学思想方法,利用图1中边长分别为a、b的两个正方形纸片和长为b、宽为a的长方形纸片,可以拼出一些图形来解释某些等式,如,由图2可得(a+2b)(a+b)=a2+3ab+b2.则:
(1)由图3可以解释的等式是 (2a+b)(a+b)=2a2+3ab+b2(2a+b)(a+b)=2a2+3ab+b2;
(2)用9张边长为a的正方形纸片,12张长为b、宽为a的长方形纸片,4张边长为b的正方形纸片拼成一个大正方形,求这个大正方形的边长;
(3)用5张长为b宽为a的长方形纸片按照图4方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分的面积设为S1、S2,BC的长设为x.
①请用含x的代数式表示:2S2-3S1;
②若无论x取任何实数时,①的结果始终保持不变,请直接写出a与b满足的数量关系.
【考点】多项式乘多项式.
【答案】(2a+b)(a+b)=2a2+3ab+b2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/23 8:0:8组卷:351引用:4难度:0.5