定义：在平面直角坐标系xOy中，函数图象上到两条坐标轴的距离之积等于n （n≠0）的点，叫做该函数图象的“n阶积点“．例如，点（1，1）为反比例函数y=1x图象的“1阶积点“，（3，-32）为一次函数y=-32x+3图象的“92阶积点“．
（1）若点（-2，-2）为y关于x的二次函数y=mx2图象的“n阶积点“，则n的值等于 44，m的值等于 -12-12；
（2）若y关于x的一次函数y=mx+2的图象经过一次函数y=x-1图象的“2阶积点”，求m的值；
（3）若y关于x的一次函数y=nx+3n-6图象的“n阶积点“恰好有3个，求n的值．
1
x
3
2
3
2
9
2
1
2
1
2
【答案】4；-
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/19 8:0:9组卷：337引用：1难度：0.4
相似题
-
1．反比例函数y=
图象上有三个点（-2，y1），（-1，y2），（1，y3），则y1、y2、y3的大小关系是（ ）k2+1x发布：2024/12/23 16:30:2组卷：41引用：3难度：0.6 -
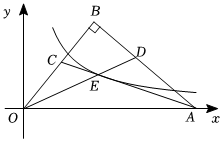2．如图，在Rt△OAB中，∠OBA=90°，OA在x轴上，AC平分∠OAB，OD平分∠AOB，AC与OD相交于点E，且OC=，CE=5，反比例函数2的图象经过点E，则k的值为 ．y=kx（k≠0，x＞0）发布：2024/12/23 19:0:2组卷：1719引用：6难度：0.5 -
3．已知点（-1，y1），（2，y2），（3，y3）在反比例函数y=-
图象上，则y1，y2，y3之间的大小关系是（ ）6x发布：2024/12/23 16:30:2组卷：51引用：4难度：0.7
