四边形ABCD是正方形，AC是对角线，E是平面内一点，且CE＜BC，过点C作FC⊥CE，且CF=CE．连接AE、AF，M是AF的中点，作射线DM交AE于点N．
（1）如图1，若点E，F分别在BC，CD边上．
求证：①∠BAE=∠DAF；
②DN⊥AE；
（2）如图2，若点E在四边形ABCD内，点F在直线BC的上方，求∠EAC与∠ADN的和的度数．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：923引用：10难度：0.5
相似题
-
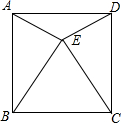1．如图，四边形ABCD是正方形，△EBC是等边三角形，求∠AED的度数．发布：2025/6/15 0:30:1组卷：239引用：7难度：0.5 -
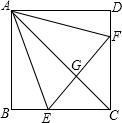2．如图，已知在正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，给出下列结论：
①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF．
其中结论正确的共有（ ）发布：2025/6/15 0:30:1组卷：1264引用：17难度：0.5 -
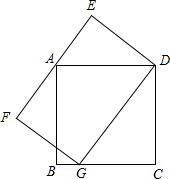3．如图，正方形ABCD的顶点A在矩形DEFG的边EF上，矩形DEFG的顶点G在正方形ABCD的边BC上，已知正方形ABCD的边长为4，DG的长为6，则DE的长为 ．发布：2025/6/15 0:0:1组卷：177引用：3难度：0.6
