在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“灵动三角形”．如，三个内角分别为120°，40°，20°的三角形是“灵动三角形”．
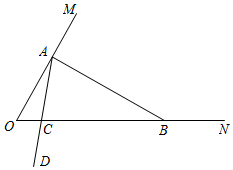
如图，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（规定0°＜∠OAC＜90°）．
（1）∠ABO的度数为3030°，△AOB是是（填“是”或“不是”）灵动三角形；
（2）若∠BAC=60°，求证：△AOC为“灵动三角形”；
（3）当△ABC为“灵动三角形”时，求∠OAC的度数．
【考点】三角形内角和定理．
【答案】30；是
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/18 5:0:8组卷：1518引用：8难度：0.5
