下面是某数学兴趣小组在项目学习课上的方案策划书，请仔细阅读，并完成相应的任务．
| 项目课题 | 探究用全等三角形解决“不用直接测量，得到高度”的问题 |
| 问题提出 | 墙上有一点A，在无法直接测量的情况下，如何得到点A的高度？ |
| 项目图纸 |
|
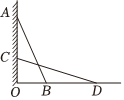
| 解决过程 | ①标记测试直杆的底端点D，测量OD的长度．②找一根长度大于OA的直杆，使直杆斜靠在墙上，且顶端与点A重合；③使直杆顶端缓慢下滑，直到∠DCO=∠ABO；④记下直杆与地面的夹角∠ABO； |
| 项目数据 | … |
（1）由于项目记录员粗心，记录排乱了“解决过程”，正确的顺序应是
D
D
；A．②→③→①→④
B．③→④→①→②
C．①→②→④→③
D．②→④→③→①
（2）线段
OD
OD
的长度，即为点A的高度；（3）请你说明他们作法的正确性．
【考点】作图—应用与设计作图；全等三角形的应用．
【答案】D；OD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/29 7:0:8组卷：78引用：7难度：0.5
相似题
-
1．我们把能二等分多边形面积的直线称为多边形的“好线”，请用无刻度的直尺作出图（1）、图（2）的“好线”．其中图（1）是一个平行四边形，图（2）由一个平行四边形和一个正方形组成．（保留作图痕迹，不写作法）
发布：2024/12/23 13:30:1组卷：205引用：7难度：0.7 -
2．在3×3的正方形格点图中有格点△ABC，请在下图1～3中分别按下列要求画出一个不同于△ABC的格点三角形．
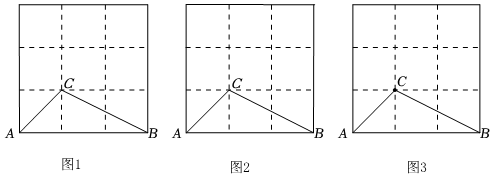
（1）在图1中画出的格点△ABD，且与△ABC面积相等．
（2）在图2中画出的格点△ACE，且与△ABC面积相等．
（3）在图3中画出的格点△BCF，且是一个轴对称图形．发布：2024/12/23 16:30:2组卷：46引用：3难度：0.6 -
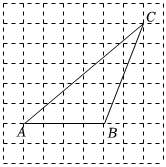3．如图，网格中的每个小正方形的边长都是1，线段交点称作格点．
（1）画出△ABC的高CD；
（2）直接写出△ABC的面积是；
（3）在线段AB上找一点E（点E在格点上），连结线段CE，使得线段CE将图中△ABC分成面积相等的两部分．发布：2024/12/23 16:0:2组卷：65引用：3难度：0.6
