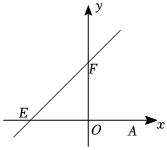
如图，直线y=kx+6与x轴、y轴分别相交于点E、F，点E的坐标为（-8，0），点A的坐标为（6，0），点P（x,y）是第一象限内的直线y=kx+6上的一个动点．（1）求K的值；
（2）在点P的运动过程中，写出△OPA的面积S与x的函数表达式，并写出自变量x的取值范围；
（3）探究，当点P运动到什么位置（求P的坐标）时，△OPA的面积是27．
【考点】一次函数图象上点的坐标特征；一次函数的性质．
【答案】（1）；
（2）；
（3）点P的坐标为（4，9）时，△OPA 的面积是27．
k
=
3
4
（2）
S
=
1
2
×
6
×
（
3
4
x
+
6
）
=
9
4
x
+
18
（
x
＞
0
）
（3）点P的坐标为（4，9）时，△OPA 的面积是27．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/7 14:0:2组卷：397引用：1难度：0.5
相似题
-
1．孔明同学在解方程组
的过程中，错把b看成了6，他其余的解题过程没有出错，解得此方程组的解为y=kx+by=-2x，又已知直线y=kx+b过点（3，1），则b的正确值应该是．x=-1y=2发布：2025/6/18 7:0:1组卷：1096引用：33难度：0.5 -
2．已知一次函数y=kx+b的图象经过A（x1，y1），B（x2，y2），且x2=1+x1时，y2=y1-2，则k等于（ ）
发布：2025/6/18 4:30:1组卷：653引用：6难度：0.7 -
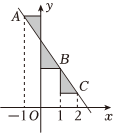3．如图，点A，B，C在一次函数y=-2x+5的图象上，它们的横坐标依次为-1，1，2，分别从这些点作x轴与y轴的垂线，则图中的阴影部分的面积之和是（ ）发布：2025/6/18 4:0:2组卷：332引用：2难度：0.9
