数学课上，同学们遇到这一个问题：

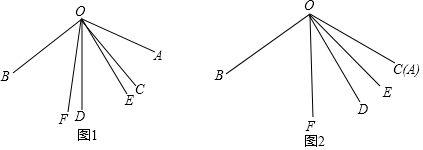
如图1，已加∠AOB=α（90°＜α＜180°），∠COD=β（0＜β＜45°），OE、OF分别是∠AOD与∠BOC的角平分线，请同学们根据题中的条件提出问题，大家一起来解决（本题出现的角均小于平角）．
同学们经过思考后，交流了自己的想法：
小强说：“如图2，若OC与OA重合，且α=120°，β=30°时，可求∠EOF的度数”．
小伟说：“在小强提出问题的前提条件下，将∠COD的OC边从OA边开始绕点O逆时针转动m°（0＜m＜30），可求出

∠

BOE

-

∠

DOF

∠

EOF

的值”；
老师说：“在原题的条件下，借助射线OC、OD的不同位置可得出α、β、∠EOF三者之间的数量关系．”
…

（1）请解决小强提出的问题；
（2）在备用图1中，补充完整的图形，并解决小伟提出的问题；
（3）在备用图2中，补充完整的图形，并解决老师提出的问题，即求出α、β、∠EOF三者之间的数量关系．